Acceleration: A Change in the Change in Motion

Table of Contents

What is Acceleration?

The change in speed or velocity of a body in motion gives rise to the concept of acceleration. A bike changes its gear and comes to high or low speeds. Similarly, the speed of a train is different as it approaches towards or leaves the station. Hence, a sudden change is brought in the motion of objects. This change is known as acceleration.

Physics defines acceleration as the rate of change of velocity over time. This means that acceleration is the further change in speed/velocity. Velocity itself is a change in motion of an object. Therefore, acceleration is the change in the change in motion. The acceleration can also have three reasons for occurrence:

If the speed is increasing,
If the speed is decreasing,
If the speed is uniform but direction changes.

This decreasing speed gives negative acceleration called the retardation. In circular motions or lets say if a car is travelling on a curved road but the speed is constant, its direction is changing continuously. Thus, the car is still said to be accelerating.

Acceleration therefore, not only occurs with change in speed but also with the change in direction. It cares both about magnitude of speed and also the direction . Hence, acceleration is clearly a vector quantity. Two objects moving with same speeds can have different acceleration if their direction is changing differently. Similarly, acceleration is also not always increasing but decreasing also.

Acceleration is also among fundamental concepts of motion. It plays a major role in describing motion, forces, and many natural phenomena like falling objects, moving objects and also the motion of planets.

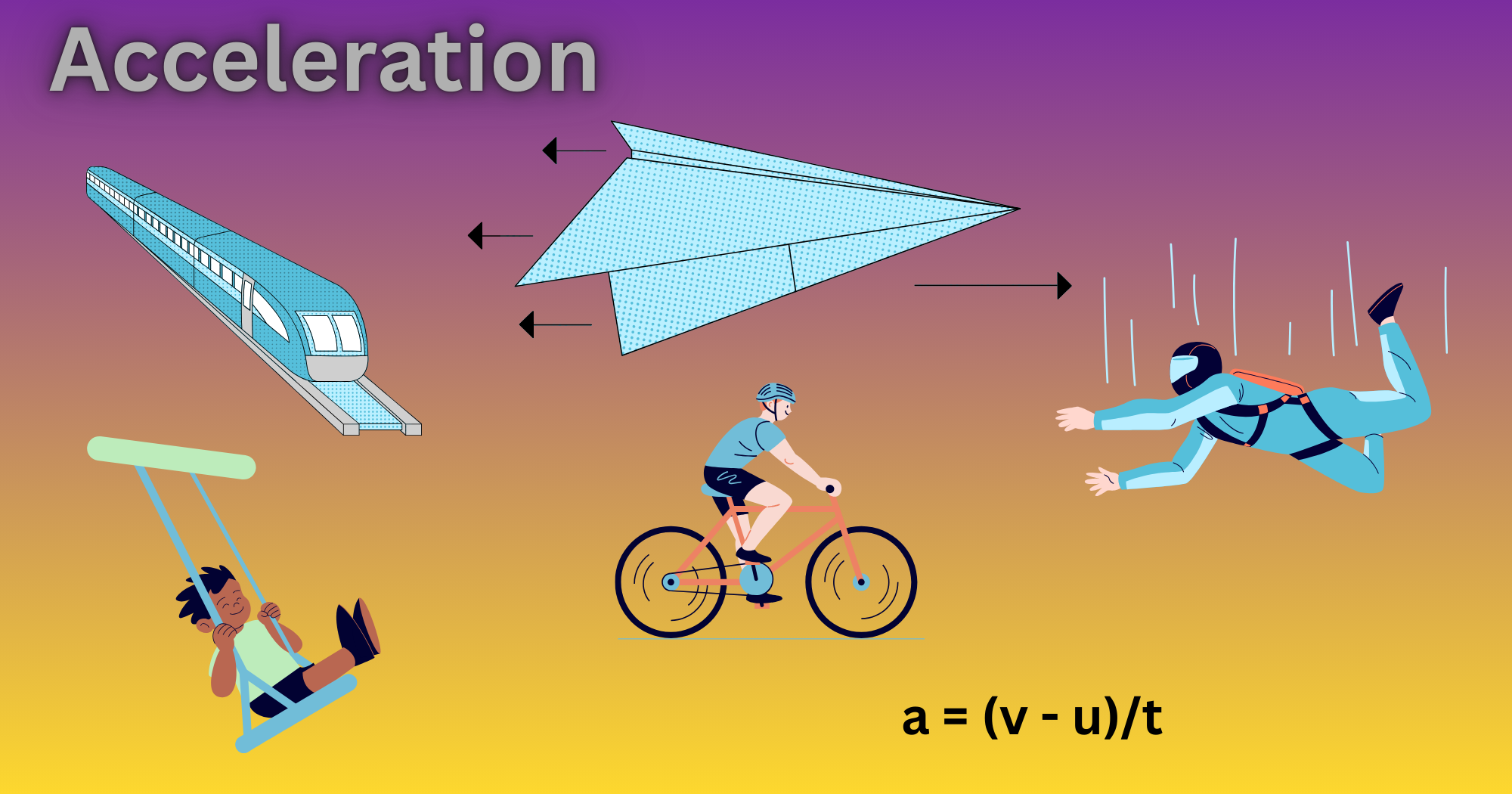
The Acceleration Formula: Calculating Change in Velocity over Time

Mathematically,

Acceleration = Change in velocity / Time taken [Equation 1]

We can also write,

a = (v − u) / t [Equation 2]]

Where:

a = acceleration
u = initial velocity (starting velocity)
v = final velocity (ending velocity)
t = time taken

Thus, from equation (2) we can say that the acceleration depends on two things:

Change in velocity (acceleration is directly proportional to the change in velocity)
Time taken (acceleration is inversely proportional to the length of time for the motion)

Also, if the change in velocity is larger, the acceleration will be greater and if the time taken is greater, acceleration will be smaller.

Dimensional Formula:From the formula in equation (1) as velocity is measured in meters per second, we can write it as [LT⁻¹] and time as [T]. Finally, the dimensional formula for acceleration becomes, [LT⁻²].

SI Units of Acceleration: Meters per Second Squared (m/s²)

The SI unit of acceleration is meters per second squared m/s² (or m s⁻²). Since velocity is measured in meters per second (m/s), the acceleration becomes m/s per second. Therefore, the unit becomes m/s².

Usually, we are not used to using the unit m/s² directly. However, we will be talking about the change in speed in m/s or km/h. The same thing in physics is given the name as acceleration (m/s²) because it clearly mentions how the speed is changing.

Acceleration vs. Velocity: Understanding the Difference

Speed, velocity and acceleration are quite confusing terms. So a learner should be made clear about all these concepts to understand motion undoubtedly. However all three terms are closely related.

An object has a velocity means the object is moving at a rate, towards the path, in a certain direction. An object cannot have acceleration but still may have a velocity in linear motions. This case happens if the object is moving at uniform velocity. As there is no change in velocity, acceleration will be zero.
Acceleration occurs only if change in velocity arises. An object can have constant velocity and also acceleration in case of circular motion. Here, the change in direction also assigns acceleration to the object.
From velocity we can tell how fast the object is moving while by acceleration we can tell how quickly the velocity is changing and in which direction that change is happening.
Finally, velocity gives the position and direction of a motion while acceleration gives the change in the position and direction of a motion.

In physics, the pace of motion and change in that pace of motion are relatable but different concepts. Various laws of motion, mechanics and dynamics are on the basis of acceleration also. Therefore, recognizing both uniquely is very important to correctly grasp physics.

Uniform and Non-Uniform Acceleration Explained

As like speed and velocity, acceleration is also of two types:

Uniform Acceleration

Uniform acceleration is the acceleration of a motion when the body in motion makes equal changes in the velocity in equal intervals of time. Therefore for uniform acceleration,

The acceleration remains constant.
The velocity increases or decreases constantly.

A common example is a body falling under the influence of gravity.

Non-Uniform Acceleration

Non-uniform acceleration is the acceleration of a motion when the body in motion makes the change of velocity unequally in the same time intervals.Therefore for non-uniform acceleration,

The acceleration is varying.
The velocity may increase or decrease unequally.

For example, a car speeds-up on open easy roads, slows down in turns and packed roads and stops at various signals.

Uniform acceleration is an ideal acceleration which is obtained in falling objects while non-uniform motion is the daily circumstance and is much more common.

Deceleration: The Concept of Negative Acceleration

Deceleration is the opposite of acceleration. It means that the change in velocity of the motion becomes negative. Therefore, if the final velocity is smaller than the initial velocity of any motion, then we obtain deceleration or retardation. For example, if a ball is hit in the ground, first it moves faster, attains a maximum velocity and then starts to slow down until it comes to rest. From this instance we can say that first the motion is accelerating and after reaching maximum velocity it starts decelerating before coming to rest.

From equation (2)
a = (v − u) / t

Therefore, mathematically also, if v is smaller than u, the numerator becomes negative, and hence we get a negative acceleration. Therefore, deceleration doesn’t mean a complex context but a decreasing acceleration than the initial condition.

Interpreting Velocity-Time Graphs: Finding Acceleration from Slope

Velocity-time graphs are the graphs made by taking different velocities of a moving object at various time periods. In graphical methods, time is kept along the x-axis and velocity is kept along the y-axis.

Slope of the Graph

Slope of the graph is calculated as:

Slope = change in y-axis / change in x-axis [Equation 3]

In the velocity-time graph, as x-axis represents time and y-axis represents velocity, the magnitude of slope becomes, change in velocity / change in time. Therefore, the slope of a velocity-time graph represents the acceleration of that motion.

If the graph is a straight line with positive slope, acceleration is constant and positive.
If the graph is a straight line with negative slope, acceleration is constant but negative i.e. retardation or deceleration.
A curved line means that the acceleration is non-uniform.
If we obtain a horizontal straight line, then we conclude that the object is at zero acceleration and constant velocity.

Acceleration Due to Gravity: Free Fall and the Constant g

An object when thrown upward, inside the earth falls down due to the gravitational force of earth. Thus, a falling object experiences a constant motion. This fall is only due to the gravity of earth, which is called the free-fall. This falling object changes its velocity constantly. Thus, a constant change in velocity will give rise to a uniform acceleration. As the acceleration is solely due to gravity, it is called the acceleration due to gravity. It is denoted by ‘g’ and is calculated by using the formula;

g = GM/R² [Equation 6]

Where,

G = universal gravitational constant (6.67×10^-11Nm²/kg²)

M = mass of the body

R = radius of the body

From equation (6), g is found to have an inversely proportional relation with the square of radius of any object.

Celestial objects have their own acceleration due to gravity. For earth, its value is found to be approximately 9.8 m/s². It means that every falling object on earth will have a constant change in velocity by 9.8 m/s, every second.

Interesting facts about the acceleration due to gravity of earth are:

The value of ‘g’ decreases while going to higher altitudes from the surface.
The value of ‘g’ also decreases on going towards the depth of the earth.
The value of ‘g’ becomes zero at the center.

Hence, ‘g’ is highly effective on the surface of the earth. On the surface also, earth being of oblate shape, the equator and poles are of different radii. Hence, the value of ‘g’ differs a little, accordingly.

The Relationship Between Force, Mass, and Acceleration

In dynamics, acceleration plays a great role to define a force. Force was first introduced by Newton and among his three laws, Newton’s second law is also called the real law of motion. In the second law he established a mathematical relation between force and acceleration as:

F = m a [Equation 4]

Where:

F = net force acting on the object
m = mass of the object
a = acceleration of the object

From equation (4) we can write: a = F/m.

Hence, a greater force gives greater acceleration but in opposition, a greater mass gives less acceleration.

If net force is zero then in equation (1), ma = 0. Since, mass always remains constant, acceleration becomes zero. This means that, for a body in motion with net force zero, the body has a uniform velocity and hence, it has no acceleration.

This law explains why:

A football accelerates quickly when kicked.
A heavy truck accelerates slowly with the same engine force.
Stronger engines give cars greater acceleration.

Lastly, from this law we can conclude that, for a body to make change in velocity, a force is required (Newton’s first law). The force directly affects the acceleration.

Centripetal Acceleration: Acceleration in Circular Motion

In circular motion, an object is moving in a circular path. Here, the object has an angular displacement and hence angular velocity. But whether the object is moving with uniform or non-uniform velocity, it always has an acceleration. This acceleration comes from the change in direction while travelling around the circle. This circular acceleration is known as the centripetal acceleration. This acceleration is always directed towards the center of the path.

Mathematically, centripetal acceleration is expressed as: a = v²/r [Equation 5]

Here, v = velocity of the moving object

r = radius of the circular path

This acceleration gives rise to a force called centripetal force. Mathematically, as F = ma and from equation (5) we have, a = v²/r, we get the expression for centripetal force as,

F_c = mv²/r [Equation 6]

This force is responsible for holding the circular motion. Hence, without the centripetal acceleration, this force would not arise and hence the circular motion would not be possible. Moreover, we can conclude that an acceleration can also pop out if there is only change in direction of motion.

Conclusion

Acceleration has also become a core concept of physics. It depends on both speed and direction of a moving object. It arises when any external force changes the velocity or direction of an object, as per Newton’s second law. The linear and circular motions have different physics for the rise of acceleration. The change in velocity (either uniform or non-uniform) determines the type of acceleration produced in an object.

A graphical representation of the change in velocity and time is a strong way to understand the motion and the concept of acceleration. A normal linear acceleration and a centripetal acceleration have different descriptions of a motion. The resulting forces also have different significance. All the circular motions are held due to centripetal accelerations, but the linear motions may have zero accelerations.

The gravity also contributes to an acceleration, which describes the motion of falling objects. It is uniform though. Hence, from real life motions to some unseen ideal motions, acceleration plays a crucial motion that defines a force. Study of acceleration is the foremost in physics, engineering and advanced physics.

References

Kleppner, D., & Kolenkow, R. (2014). An introduction to mechanics. Cambridge University Press.

Den Hartog, J. P. (1961). Mechanics. Courier Corporation.

Signell, P. (2002). Acceleration and force in circular motion. Project Physnet. Documento digital em formato PDF. East Lasing/MI: Michigan University.

Irani, A. (2022). Gravity, Density, Acceleration, and the Constants of Nature. Journal of High Energy Physics, Gravitation and Cosmology, 9(1), 210-215.

Newton, I. (2017). Laws of Motion. Law of Gravitation.

https://en.wikipedia.org/wiki/Acceleration

https://byjus.com/physics/acceleration