Biot-Savart Law: Principle, Applications, Limitations, Examples

Table of Contents

What is the Biot-Savart Law?

The Biot-Savart Law is a principle in electromagnetism that deals with the quantitative and qualitative nature of magnetic fields produced by a steady electric current. Hence it provides an empirical relationship between the electric current (I) and the magnetic field (B) that the current induces. It shows the direct association of the magnetic field with the amplitude, path, length, and location of the current. The Biot-Savart law is in strong agreement with both Ampere’s circuital law and Gauss’ theorem. The Biot-Savart law is extremely important in magnetostatics just like Coulomb’s law in electrostatics.

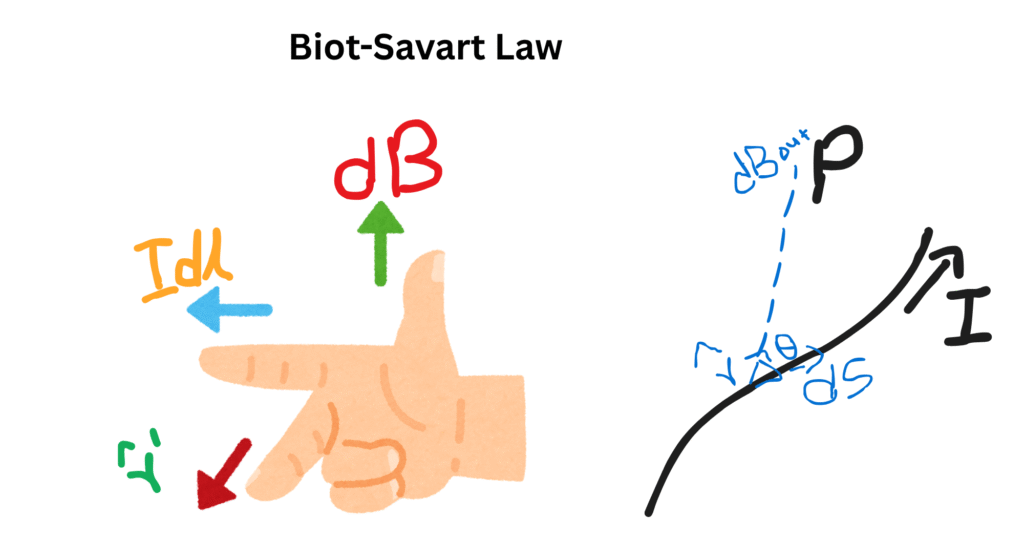
Jean Baptiste Biot and Felix Savart, combinedly gave a formula for the magnetic flux density at a point which is the result of a neighbouring current-carrying conductor. A number of calculations and observations of their work gave a conclusion that the magnetic flux density is directly proportional to the small length of the current element, current through the conductor and the sine of angle (θ) between the direction of the current and their distance vector. If dB is the magnetic flux density, dl′ is the length of current element, I be the current and (θ) is the respective angle, then the law mathematical statement of the law is given as,

dB = k Idl′sinθ/r² [Equation 1]

Here k is the proportionality constant which is equal to μ₀/4π and μ₀ is called the permeability of the free space.

It is necessary in calculating the magnetic field created by current-carrying conductors of multiple shapes. Hence we can say that this law gives a mathematical relation of the magnetic field, and the current source involved for its production.

Historical Background: Biot and Savart’s Contribution to Electromagnetism

Biot-Savart law is a spark of the well-known physical law known as Oerested law which describes the generation of magnetic fields by electric current. In 21 April, 1820, Danish physicist, Hans Christian Ørsted gave a statement “the electric current induced magnetic lines of force” after observing the fact that a needle of compass kept closer to a conducting wire showed a deflection, perpendicular to the wire.Thus his statement can be considered as the first theory that showed the mutual relation of electric current and magnetic fields.

Biot and Savart started investigating on the the Ørsted law and found major physical facts based on their experiments as follows:

The magnetic field depends on the distance from the conducting wire.
The direction of the field follows a circular pattern around the wire.
The strength of the field is proportional to the current and inversely proportional to the square of the distance from the wire.

Finally, Biot and Savart developed the empirical relation between current and magnetic field.

Mathematical Expression of the Biot-Savart Law

Considering magnetic field B at a point in space due to infinitesimally small length of current-carrying conductor, the expression for Biot-Savart Law in vector notation is given as:

B=μ₀/4π∫Idl′×r^/r²

where:

B is the infinitesimal magnetic field at a point due to a small current element,
μ0 is the permeability of free space,
I is the electric current,
dl is the infinitesimal length element of the current-carrying conductor,
r^ is the unit vector from the current element to the point of observation and
r is the distance from the element to the point.

Understanding the Variables in the Biot-Savart Equation

All the variables in Biot-Savart Law have their own significance which is pointed below:

The permeability constant provides the strength of the magnetic field to penetrate in the free space.
The current is the first requirement to get the magnetic field.
The infinitesimal current element is like a sample that contributes to the magnetic field which is absolutely based on the orientation and direction of the current..
The displacement vector determines the direction of the magnetic field passing in space.
The cross-product indicates that the magnetic field is perpendicular to both the current element and the displacement vector.

Applications of the Biot-Savart Law in Electromagnetism

As Biot-Savart Law provides the direction, path, location and all physical properties of the magnetic field induced by a current, it has a number of applications in physics and electromagnetism. Some of its applications are mentioned below:

It helps to calculate the magnetic field induced around an infinite straight conductor carrying a steady current.
Magnetic Field of a Circular Loop: It helps to determine the field generated at the center and along the axis of a circular loop carrying a current.
Magnetic Field of a Solenoid: As a solenoid can be considered having several loops, by summing up the field at multiple loops, the Biot-Savart Law can be used to measure the uniform field inside a solenoid.
Biot-Savart law is used in aerospace engineering to design magnetic shielding and control systems for spacecraft.
It helps in medical imaging systems to understand the magnetic fields generated by currents in the machines like MRI and ECG.

Derivation of the Biot-Savart Law from Maxwell’s Equations

The Biot-Savart Law can be derived from Maxwell’s equations and the Ampère’s Circuital Law in differential form with the correct suppositions. First of all, the current must be steady. For this, the electric-field should not vary with time so that the charge distribution is even. Thus, the magnetic field should also be static.

The famous Maxwell’s equation in magnetostatics is given as:

∇×B=μ₀J [Equation 2]

Here, B is the magnetic field and J is the current density vector.
Also, the divergence of a magnetic field is 0 i.e.

∇⋅B=0 [Equation 3]

Using the curl of a vector potential to express B we get,

B=∇×A [Equation 4]

Thus, applying equation [4] in [3] we get,

∇×(∇×A)=μ₀J [Equation 5]

Now, using vector identity, ∇×(∇×A) = ∇(∇⋅A)−∇²A in [5] and setting ∇⋅A = 0, we will have,

−∇²A=μ₀J [Equation 6]

Equation [6] is known as the Poisson’s equation for each component of A whose general solution is;

A(r)=μ₀/4π∫J(r′)/∣r−r′∣d³r′ [Equation 7]

Where: r is the field point where we want to calculate the field and r′ is the point source where the current is located. Again, using [7] in [4] we get,

B(r)=μ₀/4π∫J(r′)×∇(1/∣r−r′∣)d³r′ [Equation 8]

Using the identity: ∇(1/∣r−r′∣)=−r−r′/∣r−r′∣³ we get,

B(r)=μ₀/4π∫J(r′)×(r−r′)/∣r−r′∣³d³r′ [Equation 9]

Assuming that the wire is thin with current I flowing through it, we put J(r′)d^3r′ as Idl′.

Finally, with all above expressions and suppositions we get the expression for Biot-Savart law as:

B(r)=μ₀/4πI∫dl′×(r−r′)/∣r−r′∣^³ [Equation 10]

Limitations and Assumptions of the Biot-Savart Law

Although Biot-Savart law is highly useful, its applications are limited and can’t be useful in certain criterias. Some of the limitations of this law are written below:

It is valid only for steady currents. Therefore, the current should not vary with time so that a uniform charge is distributed throughout.
It can’t be applied to the conductors where alternating current is provided.
It holds accurately for only infinitesimal current elements.
The law simply applies to magnetostatics and avoids relativistic effects.

Comparison Between Biot-Savart Law and Ampère’s Law

Both laws provide the relationship between electric currents and magnetic fields. However the differences between them are compared below:

Biot-Savart Law is a mathematical tool that gives the magnetic field produced at a point due to an infinitesimal element of the current-carrying conductor while Ampere’s law is a statement which states that the total current traveling through a closed loop is proportional to the overall magnetic field around it. The expression for Ampere’s Law is given as:

∮B⋅dl=μ₀I [Equation 11]

Ampère’s Law is an integral form that gives a total magnetic field inside a closed loop while Biot-Savart Law is a differential law that gives magnetic field due to a small element of current.
Biot-Savart law is a bit complex which requires knowledge of vector calculus and integrations while Ampere’s law is quite simple and doesn’t require full integration all the time.
Biot-Savart law doesn’t require symmetry and is applicable for any shape while Ampere’s law requires symmetrical current distribution.

Practical Examples: Calculating Magnetic Fields Using the Biot-Savart Law

Using the Biot-Savart Law, we can calculate the magnetic field at the center of a current-carrying loop as:

B=μ₀I/2R.

Here, R is the radius of the loop and I is the current in the loop.

Similarly, we can also find magnetic field on the axis of a circular loop, at a distance x from its as:

B=μ₀IR²/2(R²+x²)^3/2

We can apply the law to calculate the magnetic field due to an infinite straight current-carrying wire:

B=μ₀I/2πR

Conclusion

The Biot-Savart Law is a very basic and key principle of electromagnetism. It gives some important information on how electric currents generate magnetic fields. Although it has certain limitations like steady currents and magnetostatics, it is still a powerful mathematical tool for evaluating magnetic field distributions. Its applications cover physics, engineering, and medical science. Thus, its wide applications prove that it has a vital role in both theoretical and practical fields. (Also read about Faraday’s law and Lenz’s law)

References

Phillips, J. A., & Sanny, J. (2008). The Biot-Savart law: From infinitesimal to infinite. The Physics Teacher, 46(1), 44-47.

Cavalleri, G., Spavieri, G., & Spinelli, G. (1996). The ampere and biot-savart force laws. european Journal of Physics, 17(4), 205.

Caravaca, M., Abad, J., & Catalá, J. D. (2015). Biot-Savart law as a tool to calculate the matrix of inductances and the coupling coefficient of two coaxial solenoids with arbitrary cross sections. International Journal of Electrical Engineering Education, 52(3), 237-247.

https://www.sciencefacts.net/biot-savart-law.html

https://www.geeksforgeeks.org/physics/biot-savart-law/

Biot Savart Law: Statement, Derivation An Applications