Introduction to Centre of Mass
Every object having mass is concentrated to its core called the ‘Centre of Mass’. Even a lightweight cotton to a heavy car or let’s say our earth also contains a point where all mass is fixed. This point is called the centre of mass. The whole mass of a body can be distributed into several parts with different directions. However, the whole mass can be resolved only by studying the property of the centre of mass. For example, a long stick can be balanced by our hand in an equilibrium position. This is possible only if the stick is kept in its centre of mass.
This concept of centre of mass has made it easier to solve many complex systems involving several unique particles. As these particles can be studied under a single centre of mass, this idea is used by engineers, physicists, architects etc. to design vehicles, buildings etc. Also athletes and gymnasts use it to balance their body.
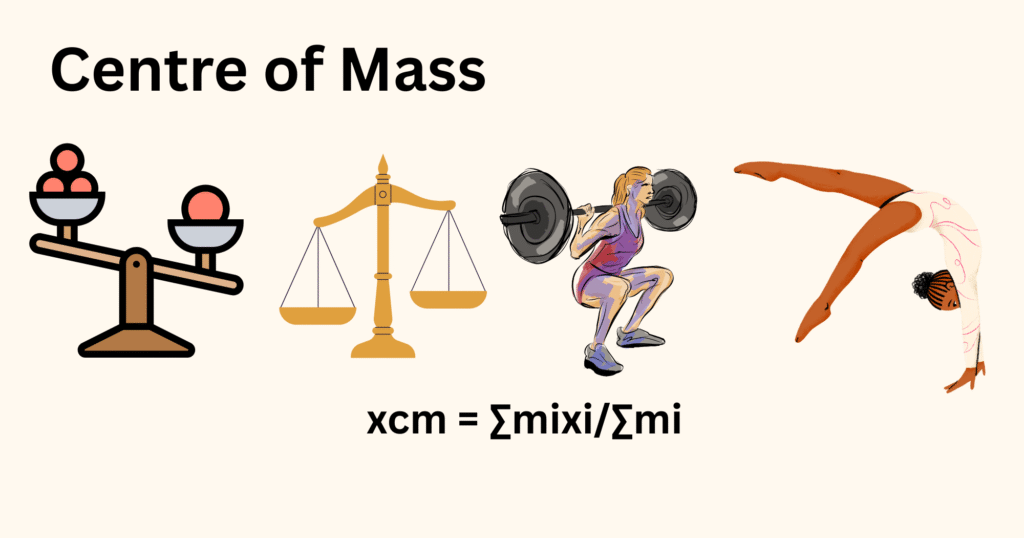
Definition and Physical Meaning of Centre of Mass
To study translational motion of a body, we can consider the centre of mass of that body where all the body’s mass remains focused as, like, a nucleus of the biological cell or the nucleus of an atom. While it is not fixed that the centre of mass always lies in the centre or inside the body. It is determined by the distribution of the mass of that body.
Simply, it can be understood that it is a balance or equilibrium point of an object. Thus, if we keep a body suspended at exactly its centre of mass, the body will hang in its perfect equilibrium position. Examples may include a uniform ruler whose centre of mass is at the midpoint, a hammer heavier on one side which has its centre of mass at some point closer to the head, a donut-shaped ring having the centre of mass at the empty center.
The centre of mass is not fixed. It depends on the shape and mass distribution of that object. For living objects it also depends upon the posture or orientation of that object. A person standing normally has a centre of mass around the stomach area, but the point shifts when the person bends, raises arms or sits down.
Difference Between Centre of Mass and Centre of Gravity
Huge confusion lies among the minds when the gossip is about centre of mass and centre of gravity. However, both meanings have vast differences. We know, mass and weight are two different physical quantities. Mass of an object remains constant, whatever be the condition, but weight is the action of gravity and keeps changing as the acceleration due to gravity changes from point to point. Centre of mass is also the quantity that depends only on mass while centre of gravity depends upon weight of the object.
Centre of Mass (COM):
- Depends only on the mass and its distribution in an object.
- It can be calculated even in space where gravity is minimum or zero..
Centre of Gravity (COG):
- Depends on the weight of an object and its distribution on a mass.
- If the gravitational field changes, the centre of gravity also changes.
Note: Centre of gravity and centre of mass can be practically same, if the acceleration due to gravity is uniform around a surface.For e.g. the value of ‘g’ is uniform around earth’s surface.Thus the centre of mass and centre of gravity are practically the same in earth. But if the gravitational field varies across the object (for very large bodies), the two points may differ.
For Example:
- In space, an astronaut floating in zero gravity has no “centre of gravity,” but the astronaut still contains a center of mass.’
- Gravity changes a little from the top to the bottom of big things like mountains and tall buildings.
Mathematical Representation of Centre of Mass
The center of mass of a body can be calculated by taking the summations of the product of the masses and their positions.
For a two-body system:
If two particles of masses m1 and m2 are located at positions x1 and x2, then the centre of mass can be calculated as:
xcm = (m1x1+m2x2)/m1+m2 [Equation 1]
This formula shows that the centre of mass has a direct relation to the body’s mass i.e.
- The body with greater mass has its centre of mass closer to itself.
- Between the two masses, the center of mass lies along the middle of the line joining them.
For three or more body system:
xcm = ∑mixi/∑mi [Equation 2]
Similarly, along the y-axis and z-axes the centre of mass is given as:
ycm=∑miyi/∑miy [Equation 3]
zcm=∑mizi/∑miz [Equation 4]
For continuous bodies (shapes):
For bodies of fixed geometrical shape and having symmetrical and uniform composition like rods, spheres, cylinders etc. the centre of mass is calculated as
xcm=1/M ∫x dm [Equation 5]
For a system of particles lying along a same line, like a group of marbles in a bag, atoms in a molecule etc., centre of mass is calculated as the above equation 2. For example, if three particles of masses 1 kg, 2kg and three kg are along a same line at positions 1 m, 2 m and 3 m, then their centre of mass can be calculated as:
xcm = 1×1+2×2+3×3 / 1+2+3 = 1+4+9 / 6 =14/6 = 2.33
The centre of mass can be calculated to determine the balancing point for a system, stability of the system and also to understand the motion of a group of mass.
Depending upon the type of system (1D, 2D or 3D), we study the centre of mass for that system. For example, in 1D we have rods, strings etc. whereas for 2D we have sheets, plates, circular or triangular shapes etc. Similarly in 3D we have the system of spheres, cubes, buildings etc.
Centre of Mass of Rigid Bodies
A rigid body is that object whose shape is not affected by its motion and shows no deformation. A rigid body is also made up of tiny particles and while in motion, the centre of mass can describe the motion of that whole rigid body. For example, geometrical shapes like plates, rods, spherical balls, cars etc. Their centre of mass is also not fixed and depends upon the mass distribution in that body. If the body is uniform then the mass will be uniformly distributed so that the centre of mass lies at the geometrical centre. If the body is non-uniform, the centre of mass is always towards the heavier part.
Common Geometrical Shapes and Their Centre of Mass
Some common geometrical shapes have their fixed centre of mass. Some of them are given below:
- Uniform rod: The centre of mass is in the geometrical centre of the rod.
- Rectangular plate: The centre of mass is at the intersecting point of the diagonals.
- Triangular lamina: The centre of mass is at the centroid.
- Ring: The centre of mass is at the center of the ring, where there is no mass.
- Sphere and cylinder: The centre of mass is at the geometrical center.
- Semi-circular plate:The centre of mass is located along the vertical axis but at a certain distance from the base but not at the centre.
This fixed information helps engineers to directly confirm the point of centre of mass while making a design..
Motion of the Centre of Mass
Motion of the centre of mass gives the information of the motion of the whole body. Therefore, whatever be the nature of the motion of other masses, they are represented as a whole by a centre of mass. For a body in a translational motion, the centre of mass moves in a straight line.
Also, for rotational motion, the centre of mass may remain fixed while the body spins around it.
For example, we see a baton spinning when thrown in air. However, its centre of mass is always directed towards a smooth parabolic path. When certain internal forces act on a system for a short duration-like muscles stretching or wheels rotating, they do not change the motion of the centre of mass. Its motion is affected only by the gravity or a friction.
Conservation of Momentum and Centre of Mass
The centre of mass also is in accordance with the law of conservation of momentum. When no external force is acting on a system, then the centre of mass will be moving with a constant velocity and not changing its direction. Therefore, it maintains a constant momentum.
For example, when a bomb explodes, its fragments will be blown in different directions but the centre of mass will always follow a smooth path. The same concepts lie behind the propulsion of a rocket or a spacecraft. Hence it is a widely used concept in physics and engineering for understanding flights, space missions etc.
Applications of Centre of Mass in Daily Life
The centre of mass influences many daily activities:
- Balancing and stability
The centre of mass is a highly used concept to approximate the stability or a balancing point of any body. As much as the centre of mass is kept lower, the object becomes more stable. Cars and bikes are designed with low centres of mass to prevent overturning. Gymnasts maintain their balance of the body by knowing the centre of mass.
- Sports
Athletes adjust their center of mass to give better performance. High jumpers bend their bodies so that their center of mass slides beneath the bar. Skaters also manage the mass distribution of their body and adjust centre of mass by pulling their arms inwards.
- Engineering and construction
Engineers design buildings, bridges, and towers keeping the center of mass at a stable place to avoid destruction.
- Vehicles
Buses, ships, and airplanes also have their fixed center of mass which avoids tilting and improves stability.
- Robotics
Robots are allowed to walk smoothly by constantly adjusting their centre of mass.
- Space science
Understanding the centre of mass is essential for satellite orientation, spacecraft docking, and rocket movement.
Centre of Mass in Sports, Engineering, and Space Science
- Sports
Sports are the best examples of the concept of centre of mass. Some common examples are gymnastics, athletics, high jumps, skating etc. They all obtain a body balance by considering the centre of mass. They also change their body positions and gain flexibility and stability in their actions. In the see-saw two players sitting at both ends adjust their mass and balance its centre of mass.
- Engineering
Heavy machinery like cranes, hydraulic lifts etc. are able to lift heavy loads when the centre of mass of the object lies at its base support. If heavy parts are close to the base, the object has less probability to fall.
- Space Science
From micro to macro objects all revolve around their centre of mass. A satellite also rotates around its centre of mass. For exact control of the spacecraft, engines are placed closer to their center of mass. Astronauts in space keep floating under zero gravity. Therefore, they adjust their body positions to shift their centre of mass and be able to move in the desired direction.
Conclusion
The centre of mass is a key point in physics that gives us the basic concept of the behavior of objects under different forces. From a simple object like a stick or a complex hydraulic machine, all has its centre of mass. Thus, their motion can be tracked by studying the motion of their centre of mass. The systems requiring complex physics to understand their mechanism of motion can also be studied under one frame of the centre of mass. From daily life actions like sports, lifting etc. to rocket and spacecraft design, all require the same concept of centre of mass. Thus, we can say, without this concept, we cannot study the behavior of a rigid body under forces.
References
Lebedev, D. B. (1990). Control of the motion of a solid rotating about its centre of mass. Journal of Applied Mathematics and Mechanics, 54(1), 13-18.
https://allen.in/jee/physics/centre-of-mass
https://en.wikipedia.org/wiki/Center_of_mass
https://www.geeksforgeeks.org/physics/centre-of-mass
