What is Displacement in Physics?
The concept of displacement in physics arises after the introduction of distance. It is also one of the most important concepts in physics. While studying motions, it is essential to differentiate between distance and the displacement. When an object comes in motion, it changes its state. The same motion can be studied with two major concepts: distance and displacement. However, in physics distance has a simple meaning but displacement is a more precise form of distance travelled. Being a vector quantity, displacement provides more precise information about the object’s motion by also mentioning its direction.
Displacement is defined as the shortest distance between the initial position and the final position of an object. Thus, magnitude and direction are two essential components while studying displacement. The magnitude tells us how far the object has gone from its starting point, while direction tells us where the object is going with respect to its initial point.
Displacement only considers the initial and final position of an object in motion. Hence, displacement is different from distance. Displacement requires the total length of the path traveled by an object. Thus, an accurate and precise analysis of any motion can be done with the knowledge of displacement.
In physics, displacement is represented as Δx, Δr. Being a vector, an arrow is also drawn from the initial position to the final position. Understanding displacement is essential because it defines other important physical quantities like velocity, acceleration, force etc.
The SI Unit of Displacement: Meters and Directional Notation
The SI unit of displacement and distance is the same i.e. meter (m). However, displacement is a vector, it should also give information about the direction. Directional notation can be expressed in several ways. One can write displacement as the magnitude attached with directions like north, east, south or west. Moreover, in higher-levels, displacement is written in vector notation. Symbols such as Δx for linear motion or Δr for two- or three-dimensional motion are commonly used. The right and left movement of an object with the same magnitude are opposite in signs. It is common in one-dimensional systems.
Similarly, sign conventions can also be useful to denote directions for one-dimensional motion. Here, one direction can be regarded as positive and the other opposite direction as negative. For example, motion to the right may be taken as positive, while motion to the left is taken as negative. These notations play a great role in distinguishing displacement from distance as a vector quantity. Moreover, the use of direction in displacement makes the calculation exact and able to display motion in graphs or diagrams. Without direction, the information becomes incomplete and the essential characteristics of motion would be missing.
Displacement vs. Distance: Understanding the Difference
Displacement and distance look much similar. However, they show a great difference of concepts about a body’s motion. So, the knowledge about both concepts must be clear before studying any other physical changes in motion. Distance is just the total length of the path traveled by an object, while displacement keeps track of every change in position of that object while going from initial to the final point.
Distance is a scalar quantity. This means it has only magnitude and no direction. It always has a positive value. Either the path is curved or has twists or turns, the total path is always added and hence, the distance keeps increasing. By looking at that magnitude, we can only view how much the object went through and no more than that.
In contrast, displacement clearly mentions the direction of motion. This, no doubt, proves that it is a vector quantity. It cares only about the initial and final positions of movement. The length of the path taken for the motion doesn’t matter. Therefore, due to the vector rule of addition or subtraction, it can be positive, negative, or zero.
To sum up, both quantities have their own significance during calculations. The demand of a measurement may be different, so their use must be done accordingly.
Vector Quantities: Why Direction Matters in Displacement
Displacement belongs to a class of physical quantities known as vector quantities. Vector quantities are quantities that require both magnitude and direction for complete description. If direction is considered in calculations, the opposite directions easily get cancelled out. On the other hand, if direction is not considered, the magnitudes both are added. This creates a huge difference between the same motion while viewing with two different concepts of scalars and vectors.
The vector nature of motion gives an accurate characteristic of that motion. Thus, the net effect of directions on a movement may be different. This concept gets more significant when the cases are complex as in three-dimensional space.
While using vector rules, direction is first considered. Two displacements can be added only if they are in the same directions while they are subtracted for opposite directions. Thus, direction is the only factor that determines the final state of an object. Being a vector, it always comes with an arrow sign above its magnitude. Thus, visually we can find out and analyze the vector nature of that quantity.
Because displacement is a fundamental measurement of length, all other quantities like velocity, acceleration, work-done etc. depend on it for further calculation. Thus, it is a crucial concept in physics.
Calculating Displacement: Formula and Vector Addition
The calculation of displacement may look simply, but it can become complex for complex motion. Here, by complex it is meant that the motion is two or more than two dimensional. For one-dimensional motion, we can easily be analyzed by looking at the magnitude and direction of that object. For example, if an ant moves along a straight line for 5 meters and then returns back to 3 meters, then the total displacement would be 2 meters. In more complex cases involving motion in two or more dimensions, vector addition is required.
For the motions in two-dimension, the displacement is calculated by using the vector rule of addition. If an object moves in both the horizontal and vertical directions, the displacement is resolved into two components: vertical component for y-axis and horizontal component for the x-axis. Later, they are combined with the help of Pythagoras theorem and hence resultant magnitude and directions are calculated.
For example, if a man runs 3 meters west and then 2 meters north, then his total displacement is given as:
R = √ (AB)^2 + (BC)^2 = √9+4 = √13 meters
To find the direction of the displacement we use, θ = tan-1 (y/x) = tan-1 (3/2) = 56.31°. This will be the final direction from the initial position.
Displacement on a Graph: Position-Time Analysis
Graphs are simple tools that can visualize the displacement and the motion accurately. This makes it easier to understand the nature of motion. In kinematics, maximum problems are solved firstly by visualizing the problem with the help of graphs. Among various graphs, the position-time graph is frequently used. Here, time is kept along the x-axis, and the position is kept along the y-axis.
The initial and final positions of an object in that graph gives the displacement. Hence, the change in positions of that object at a certain time interval can be found from the graph. This shows us how a displacement changes over time in a simple and understandable manner.
The change of displacement with the change in time is called velocity. In a position-time graph, the slope of that graph means the change is position to the change in time. Thus, with this graph we can easily find out the velocity of that object. If the graph between position and time is a straight line, we will get a constant slope. Thus, we can assure that the velocity is uniform and vice-versa. A horizontal line of the graph means that the object is at rest with no velocity and acceleration.
If the graph goes up, the displacement is positive. This means that the object is moving in the positive direction. Similarly, for a falling graph, the displacement would be negative. The net displacement is zero if the graph goes back to its initial starting point.
Thus, it is a powerful concept to help students understand the relationship between position, displacement, velocity, and time clearly.
Fig: Position-time graph
Positive, Negative, and Zero Displacement Explained
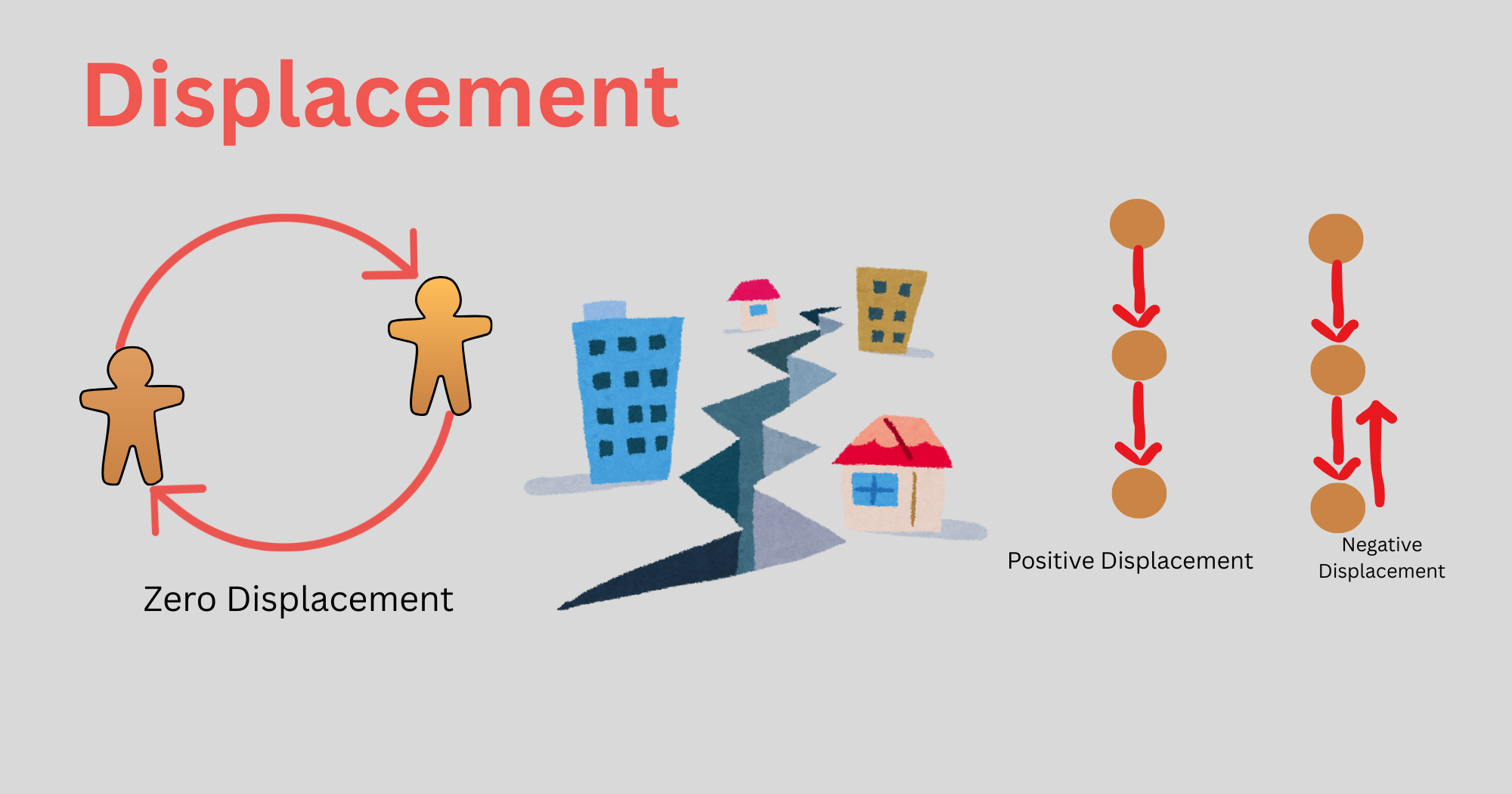
As direction plays a key role in displacement, the net displacement can be positive, negative or also zero. Thus, to accurately analyze a motion, one should be able to know in what cases such results can occur.
We call it a positive displacement if an object keeps moving in the same direction or positive direction with reference to the initial point. Similarly, we call it a negative one if the final position is in the opposite direction with respect to the initial position.
Zero displacement is the condition when the object moving from initial to final position comes back in the same direction from final position to the initial position. Thus, there will be a movement, but it means that the position of that object is not changed by the motion.
One-Dimensional vs. Two-Dimensional Displacement
A particle can be in motion in both one-dimensional and two-dimensional manner. For example, a ball rolling on a ground will have one-dimensional motion while a ball thrown with a certain angle can travel both in upward direction as well as in horizontal range. Thus, displacement depends upon the nature of motion. One-dimensional displacement involves motion along a straight line.
A one-dimensional motion is simple and can be calculated with single co-ordinates. However, for two-dimensional displacement, we need the constituent components of displacement i.e. horizontal and vertical components. The resultant of both components can only provide the magnitude of displacement. This also requires the trigonometric relation as done above.
The knowledge of both kinds of motions is equally important in kinematics and hence in physics.
Real-World Examples: Circular Motion and Return Trips
Some real-world examples which can clarify our concepts of displacement are:
- Circular motion: In circular motions, an object travels around a circle. A circle has a total length equal to the circumference of the circle (2πr). A circle does not have a starting or ending point. If an object keeps running in a circle, it may travel a distance equal to the circumference of that circle, but its net displacement is zero. It means that the object returns to the initial point along the same path after reaching the final point.
- Return trips: Return trips mean that the traveler comes to the initial point from the same path of road. For example, most of the public buses follow the same route to reach the destination and return to its initial point. Hence, how much time it may take to return, its net displacement is always zero. Also, if we go to the groceries from home and return with the same path, our net displacement will be zero.
These examples clearly prove that displacement cares only about the starting and ending point of the journey.
Conclusion
Like distance, displacement is also a fundamental concept of physics. It is also a building block of kinematics. The significance of displacement over distance is that it notes the direction. Therefore, because of vector rules and laws it only takes account of the starting and ending points of motion. The graphical representation has more significance to visualize a motion in a respective time. This is also fundamental to calculate other complex terms like velocities, acceleration etc.
The motions also have varying natures like one-dimensional or two-dimensional. They are to be solved accordingly. Hence, displacement is crucial to understand mechanics and physics. How simple it looks, it gets that complicated in higher level physics.
References
https://en.wikipedia.org/wiki/Displacement
Agrawal, A., & Redford, K. (2009). Conservation and displacement: an overview. Conservation and society, 7(1), 1-10.
Kleppner, D., & Kolenkow, R. (2014). An introduction to mechanics. Cambridge University Press.
Abou Halloun, I., & Hestenes, D. (1985). Common sense concepts about motion. American journal of physics, 53(11), 1056-1065.
Jewett, J. W., & Serway, R. (2008). Physics for scientists and engineers with modern physics. Vectors, 1(2), 633.
Displacement
