Gauss Theorem: A simple guide on its Understanding and Applications

Table of Contents

What Is Gauss’s Theorem?

Gauss’ Law is an equation or formula which was developed to describe the relation between electric charge and electric field in a stationary condition. This law becomes easier to use when the charge distribution over a surface is uniform. This law actually connects the net electric flux flowing across any closed surface to the net charge enclosed by the surface. Therefore, we can obtain a relation between the electric field and the electric charge by relating the flux and the electric field.

According to this law, ‘net electric flux (Φ) of the electric field through a closed surface is equal to 1/ε₀ times the net electric charge q_net enclosed by the surface’.

Φ = 1/ε₀ q_net [Equation 1]

In [Equation 1] ε0 is the permitivity of free space. Permitivity is a constant term which means the ability of a free space to allow electric fields to pass through it, which has the value, 8.85×10⁻¹² F⋅m⁻¹. In the case of any other medium it is denoted as ∈ and [1] can be written as

Φ = 1/ε₀ q_net [Equation 2]

The statement of Gauss theorem can also be expressed as:

∳E.ds = q/ε₀ [Equation 3]

Gauss’ theorem is also known as the divergence theorem, which is an integral analytical technique in the topic of vector analysis. This theorem got its name after the German mathematician Carl Friedrich Gauss, which describes the connection between a flux of a vector field through a closed surface and its divergence inside the volume covered by the surface. It may be defined in formulas as follows:

∫∫v∫▽F.dV = ∫∫s F.n.dS [Equation 4]

Here:

F is the vector field.
S is the closed surface enclosing the volume.
n is the unit vector normal to the surface.
▽ represents the divergence of the vector field.

As it ties the operation of a vector field on a surface with how it acts throughout the volume it encloses, this theorem is important to both the basic and the practical sciences.

Understanding the Formula of Gauss’s Theorem

To understand Gauss’s theorem in detail we have to collect some ideas about line integrals, surface integrals and volume integrals. Some key points on understanding the Gauss theorem are given below.

A function to be integrated can be operated along a curve in the coordinate system called the line integral which measures the length of the curve. Both vector fields and scalar fields can be integrated along the curve. Electric flux is a scalar quantity. In LHS of equation [3] a line integral of an electric flux in a closed surface is directly proportional to the net charge on the surface.
A function can be integrated across a surface in three dimensions and the process is known as surface integral that measures the area of the surface. The RHS of the equation [4] gives the total flux of the vector field through the closed surface. Flux gives the measure of the quantity of electric field that passes through the surface and its direction.
Volume Integral measures the volume of a function lying in a three-dimensional domain. The LHS of [4] is a volume integral over the divergence within the volume. The net rate at which the field propagates from an area is measured by divergence.

According to Gauss’s theorem, the integral of the divergence of a field over the enclosed volume is equal to the total flux of the field through a closed surface. This idea links the local characteristics of a field i.e. divergence with its overall behavior called the flux.

Applications of Gauss’s Theorem in Physics

Gauss’ Law can be used to solve complicated electromagnetic problems with unusual symmetry, such as a cylinder, spherical, or planar geometry. In other situations, figuring out the electrical field is complicated and requires a lot of integration. The following scenarios in physics can be covered by the Gauss Law.

To Calculate Electric Field in Electrostatics

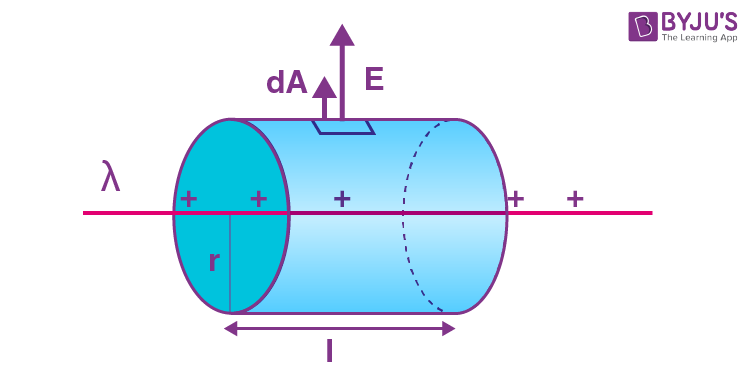
Suppose that λ is the charge per unit length of a continuously long line of charge. In this case we can apply a cylindrical symmetry. There is no component parallel to the line of charge, and all of the electric fields pass radially out from it due to the arrangement. The curved surface of the cylinder is perpendicular to the electric field. So cos θ = 1 and the angle between the area vector and electric field is zero. Once more, the cylinder’s top and bottom surfaces are parallel to the electric field. So there is an angle of 90 between the area vector and the electric field. Therefore, the curved surface is only the reason for the flow of the field. The flux is found to be,

Φ = E. 2πrl (Equation i)

Where r is the radius of the assumed cylinder and l is its length.

The net charge of the surface becomes λ.I (I being the current passing through it).

Thus, using Gauss Theorem we can find the electric field of the wire as:

E = λ/2πrε₀ (Equation ii)

In electromagnetism Maxwell’s equations are obtained and applied using Gauss’s theorem. In actual scenario, Gauss’s law in electricity plays a great role where the permittivity of free space is seen as the electric field that is the entire charge enclosed in it.

Magnetostatics

Gauss’s Theorem is used to measure magnetic flux through a closed surface as in electrostatics which is important for magnet construction and study.

Fluid Mechanics

Gauss’s theorem helps in the study of the flow of fluid in fluid mechanics like in the pipelines and ventilation. It simplifies the study of conservation of mass and momentum by relating the divergence of the vector field i.e. the velocity inside the enclosed volume to the overall flow of fluid through a closed surface.

Gravitation

The Gauss’ equation is used to determine the gravity equivalent of Gauss’s law. Gauss’ law equivalence makes the calculation of gravitational flux easier in the complex systems having spherical symmetry. Therefore, it helps in understanding how gravitational fields act, especially when calculating the mass distribution of celestial objects using gravitational flux.

Heat Transfer

Heat flow can also be examined with Gauss’s theorem. In these situations, heat production or loss within a volume is represented by the divergence, and heat transfer over a surface is represented by the flux. Knowing the thermal properties of materials and building effective cooling systems depend on Gauss’ law to analyze heat flux across surfaces in thermal engineering.

Real-World Examples of Gauss’s Theorem

There are practical applications of Gauss’s theorem in physics, medical science and other daily cases. Some of the implications are listed below:

Understanding Fields and Designing Electrical Appliances

In normal cases, we find conductors like wires, which are metal containers and block electric fields. Gauss’ Law is used to study the nature of electric fields while moving towards these conductors. The electric networks from ordinary cables to Faraday cages are made with the study of Gauss Law. Similarly appliances are allowed to run safely and effectively by this law. For example, we can use it to explain loss of signals inside the lift. Engineers use Gauss’s theorem to construct capacitors, insulators, and other devices by measuring electric flux and distribution of charges.

Medical Field

In MRI, X-ray, ECG and other machines electric fields are applied for medical imaging. These fields are sent by using Gauss’ law. It is not the main principle for the construction of these machines; rather they apply electric fields to interact with atoms in the body and create images. Gauss’s Law is required to understand these fields precisely, before applying electric fields. It is also used in radiation treatments to push the charged particles by electric fields.

Designing Particle Accelerators

In devices like particle accelerators charge particles are moved by electric fields. Gauss’ Law is applied here to build electrodes that generate the electric fields. Scientists can improve the accuracy and efficiency of particle accelerators by designing the electrodes using Gauss’ Law.

Predicting Weather Patterns

Gauss’ theorem is used to analyze the flow of the atmosphere in atmospheric physics. The flux contained in air across a region can help in estimating changes in weather conditions.

Geophysics

In geophysics, Gauss’s theorem is applied to study gravitational and magnetic fields, to gather more information about the internal structure of earth.

How Gauss’s Theorem Relates to Electric Fields

To know about electricity, first we have to gain the basic concept of electric fields. In general, Coulomb’s law is used to determine the electric field of a surface. However, Gauss law must be understood for the calculation of electric field distribution in a closed surface. It describes the electric charge that exists in a closed surface.

Gauss’s law is extremely important in conditions with strong symmetry, such as spherical, cylindrical and planar symmetries. The electric flux from any closed surface is solely due to the positive and negative charges of the electric fields contained within the surface. Any charges that exist outside the surface are not related to the electric flux.

For a point charge or uniformly charged sphere, the electric field is radial, and the flux can be easily calculated.

E = 1/4πε₀ [qx/(R²+x²)^3/2]

For an infinite line of charge, Gauss’s law simplifies the calculation of the radial electric field.

E = (1/4 × πrε₀) (2π/r) = λ/2πrε₀.

‘r’ being the radius of the ring and λ is the linear charge density.

For a uniformly charged plane, the field is perpendicular to the surface, making the application straightforward.

E = σ/2ε₀K, where σ = Surface charge density.

Deriving Gauss’s Theorem: Step-by-Step Guide

The derivation of Gauss’ theorem is not that easy and needs strict mathematical processes. It may be quite easy if the processes are broken down into steps.

The divergence of a vector field is represented by ▽.F. It represents the net flow of the electric field to a particular point.
Consider the volume enclosed by the closed surface is ‘dV’. The surface ‘dS’ is directed to be pointing outward.
Use the divergence theorem:

∫∫v∫▽F.dV = ∫∫s F.n.dS

This equation shows the relation between the surface integral of the flux and volume integral of divergence.

The result shows that the total flux across the boundary corresponds to the sum of the divergence inside.

Common Misconceptions about Gauss’s Theorem

There are various misconceptions about Gauss’ theorem. Some of them are as follows:

It is thought to be applied only to symmetrical fields. However Gauss’ theorem applies for any vector field, irrespective of symmetry which also simplifies calculations.
It is thought to be confined only to Electromagnetism. Gauss’s theorem is a broad mathematical principle that applies in many fields, including fluid dynamics and heat transfer.
It is thought that Gauss law always requires a closed surface to come into action. However in some cases like Stoke’s theorem, it handles open surfaces.

Visualizing Gauss’s Theorem with Diagrams

Visualizing Gauss’s theorem can boost our understanding of the concept. We can consider the following diagrams to visualize the theorem.

Electric Flux Through A solid conducting sphere of charge Q surrounded by an uncharged concentric conducting hollow spherical shell.

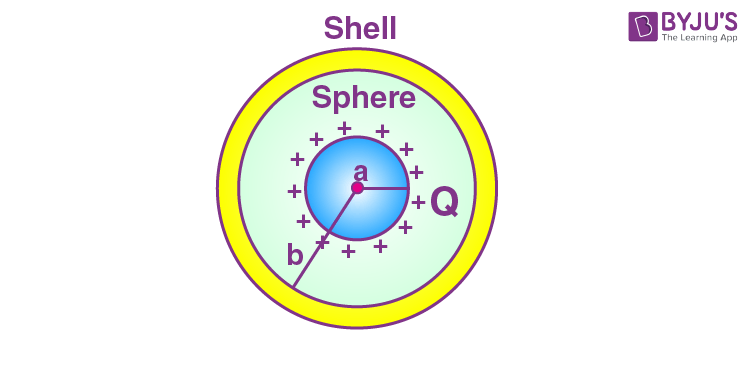
Gauss Law Applications Gauss Theorem FormulaArtboard 1 copy 10 8

Vin = Vc = Vs = 1/4πε₀

and Vout = 1/4πε₀

So, if a and b are the radii of a sphere and spherical shell, respectively, the potential at their surfaces will be

V_sphere = 1/4πε₀ [Q/a] and V_shell = 1/4πε₀ [Q/b] and so according to the given problem,

V = V’_sphere – V’_shell= Q/4πε₀ [1/a – 1/b] = V . . . . . . . (Equation a)

When charge is given to the external shell, the potential difference between the sphere and shell remains unchanged. This is because of the presence of charge on the outer shell. The potential inside and on the surface of the shell will change constantly, and hence, the potential difference between sphere and shell will remain unchanged.

Divergence in a Fluid Flow

Consider fluid moving outwards from a point. The divergence measures net flow per unit volume.

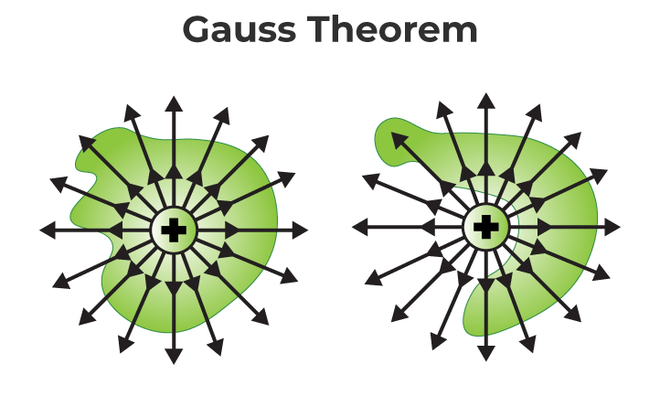
Source: https://www.geeksforgeeks.org/physics/gauss-law/

Field Lines and Flux
Field lines entering and leaving a closed surface showing flux balance.

Gauss Law Applications Gauss Theorem FormulaArtboard 1 copy 8 1

Conclusion

Gauss’ theorem is the foundation of vector analysis and physics that brings a strong bond between the local and broad features of vector fields. Its applications are diverse, ranging from electromagnetism to fluid dynamics which simplifies certain vague problems and gives new discoveries. Understanding its formula, applications, and visual interpretations gives us a strong tool for analyzing unexpected events and solving real-world problems. (Also read about Lenz’s Law)

References

Eyal, O., & Goldstein, A. (2019). Gauss’ law for moving charges from first principles. Results in Physics, 14, 102454.

Ling, S. J., Moebs, W., & Sanny, J. (2016). 6.3 Applying Gauss’s Law. University Physics Volume 2.

Balachandran, A. P., & Reyes-Lega, A. F. (2019). The gauss law: A tale. Classical and Quantum Physics: 60 Years Alberto Ibort Fest Geometry, Dynamics, and Control, 41-55.

Li, J., & Singh, C. (2017). Investigating and improving introductory physics students’ understanding of symmetry and Gauss’s law. European Journal of Physics, 39(1), 015702.

Gauss’s Law

https://www.geeksforgeeks.org/physics/gauss-law/

https://byjus.com/jee/gauss-law/