Introduction to Newton’s Law of Universal Gravitation
Sir Isaac Newton has done remarkable work in physics, giving a profound theory of gravitation. It associates the gravitational force with masses of two objects and their separation. According to this law, a mass attracts another approaching mass with a certain amount of force which is known as gravitational force. Generally, every object in the universe is attracting the other, but the force of attraction between two tiny masses far away from each other have negligible amount of force on each other and remain undetected.
It is the weakest force in nature. However, the effect of gravitation is tremendous in massive, celestial objects and Newton’s law cannot describe this force. Despite this fact, Newton’s law is seen in ordinary situations and works accurately for cases inside earth. The classical treatment of gravity has remained as a base for astrophysics, general theory of relativity, cosmology and many other branches of physics.
The Inverse Square Law: Understanding the Force-Distance Relationship
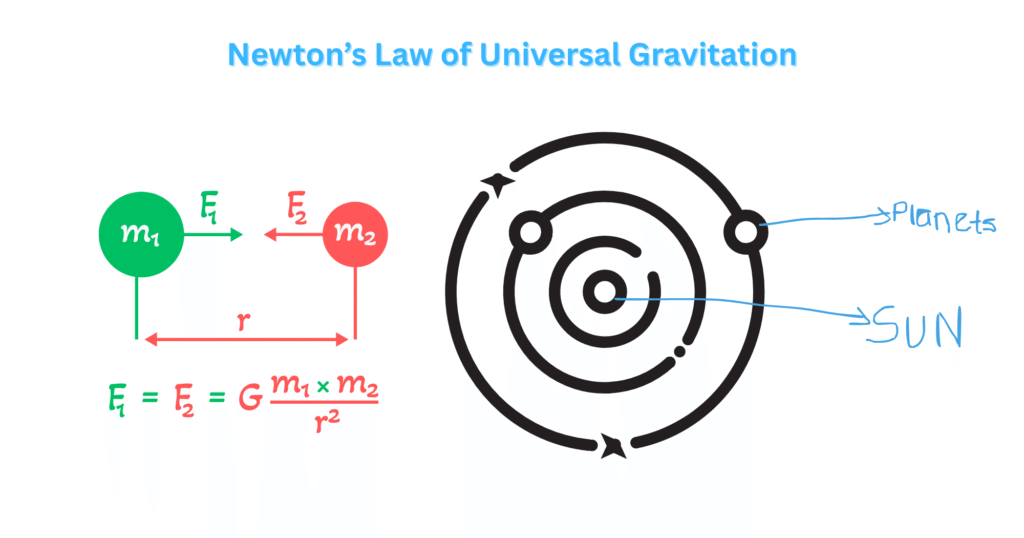
The inverse square law states that the gravitational force is directly proportional to the masses of two bodies attracting each other and inversely proportional to the square of the distance between them.
F = G * (m1 * m2) / r2 [Equation 1]
where F is the gravitational force between two masses m1 and m2, r is the distance between the centers of the two masses, and G is the gravitational constant. This law shows that if the separation of two objects is now doubled than before, the gravitational force decreases by fourth power. This law is called inverse square law. It is important to calculate and keep track of the gravitational pull of entities around us.
Calculating Gravitational Force: The Role of Mass and Distance
Calculating the gravitational force is easier if the masses and their separating distance is known. Both play a significant role in producing the amount of force. We see from equation [1], force is in proportional relation with mass and distance. If the two objects are relatively larger, they produce a greater pull, considering the distance between them is smaller. On increasing the distance, the strength of force goes on decreasing. Ordinary particles inside earth are of small masses, the force of gravity between them is small. However, the mass of particles is negligible if compared to earth. Therefore, every particle is pulled down by earth. The earth also makes the moon revolve around it, due to its heavier mass. Thus gravitational force of attraction is solely a property of attraction of a mass that can show its impact to a certain range.
The Gravitational Constant (G): Its Value and Significance
Gravitational constant appears in Newton’s universal law of gravitation as a proportionality constant. It is a very weak quantity having value 6.674 × 10^-11 N(m/kg)^2. This tiny value also describes the weak nature of gravitational force. But, when we are driving towards the celestial bodies, this small value also heavily affects the gravitational force.
The value of G applied in calculation, provides an accurate value of the force. It is employed in both classical and modern physics. Thus, G describes the strength of gravitational force.
Historical Insights: Newton’s Apple and the Birth of Gravitational Theory
Aristotle was the first person to describe the motion of objects. He believed that objects would move according to their nature. Here nature is defined according to the mass of objects. It states that heavier objects fall towards earth and lighter objects like air, fire etc, move upwards and the celestial bodies are always in their own circular motion. He assumed earth to be at the center of the sun and sun revolves around the earth. No gravity was defined and he showed no relationship between terrestrial and celestial motion.
Nicolaus Copernicus gave the right description of planetary motion and stated that earth revolves around the sun. Still the reason for this revolution was unknown. Johannes Kepler studied the motion of planets and mathematically proved that the path of these planets is elliptical. He concluded that there might be something like force which causes planets to revolve around the sun. Galileo Galilei studied about the motion of objects and their acceleration. He suggested that the mass of objects doesn’t matter their falling motion.
Newton was studying in Cambridge University and due to Plague impacts all over, the university was shut for some period. He returned home at woolsthorpe. After dinner, he wanted to roam around the garden where he saw an apple falling from a tree. Looking at the motion of the apple he started thinking about the motion of other massive objects like earth and moon. A lot of questions arose like ‘Could the moon also be falling towards earth? If not then what is holding it up there?’ These curiosities resulted in the birth of gravitational theory. This apple story was told by Newton to his friend and a biographer William Stukeley as the beginning of thoughts on motion of objects.
Later in 1678 he published a book called ‘Philosophiæ Naturalis Principia Mathematica’ where he derived the famous formula of equation [1]. On the advancements of mathematics, scientists realized a need for a constant value in Newton’s formula to provide more accurate results. In 1798, Henry Cavendish accidentally measured the value of G while determining the mass and density of earth. This G is equally used in Newton’s law and Einstein’s General Theory of Relativity.
Comparing Newtonian Gravity with Einstein’s General Relativity
No doubt, Newton’s law is a successful law to describe every motion from everyday incidents to planetary motions. But it is questionable when we talk about super massive objects and light. It couldn’t explain the precise movement of mercury around the sun. Other phenomena like bending of light and time dilation were also unanswered by Newtonian mechanics.
In 1904, with the birth of Einstein’s General Relativity, many secrets of the universe remained unfolded. He explained gravity differently rather than a force. He suggested that gravity is the result of heavier masses of bodies which curve the path around it. Other lighter bodies would move in this curved path. Space and time were taken as the dimensions of the universe and both were affected by gravity. Thus, it answered the question of time dilation. He predicted that very strong gravity also affects light and causes bending of light. Gravitational waves and gravitational lensing are two proven predictions of Einstein’s theory.
Einstein’s theory follows very complex mathematics which cannot be cracked in a simple manner. It is also proven wrong by quantum mechanics and later was modified and unified with quantum theory. It is still unable to reach deeper inside compact objects like black holes and dark matter.
Practical Applications: From Planetary Orbits to Tidal Movements
We find Newton’s law in everything around us. We are able to reside on earth due to the earth’s gravity. It has countless applications, few of them are given below:
- Motion of planets and moon: Planets are strictly following their own path around the sun. This is possible due to the gravitational pull between the sun and planets. Similarly, the moon revolves around the earth as described by Newton’s law. Nearby planets may influence each other’s orbit. This influence for a long time period can result in some disturbance in their orbit.
- Mass of planets and moon: After knowing the mass of the sun and distance between the sun and a given planet, one can easily calculate the mass of a planet. Accordingly, we can calculate the mass of the moon.
- Tidal forces: The gravitational pull of the moon and earth to the ocean’s water give rise to tides.
- Engineering: Engineers use Newton’s law to calculate the orbital speed, height and escape velocity for a satellite. They also use the law in rocket launching. Huge structures like bridges, dams etc. are constructed by studying its ability to withstand gravity.
- GPS and Navigation: GPS systems use Newton’s law in starting to calculate the orbital parameters of satellites.
- Problem Solving: Newton’s law is widely applied in physics education to calculate the mass, amount of gravitational force and position of an object.
Limitations of Newton’s Law in Modern Physics
Newton’s law also has certain limitations in advanced cases. Some of its limitations are mentioned below:
- Breaks down at strong gravity: In ordinary cases it is true but when the case appears for strong gravitational fields such as black holes, neutron stars, pulsars etc, the equation fails. Relativity correctly explains about these singularities.
- Time dilation: It couldn’t explain the time delay around strong gravitational fields like event horizons of black holes.
- Mercury precision: The orbit of mercury is slowly shifting due to the gravity of the sun that curves space-time as described by modern physics. It was unanswered by classical mechanics.
- Inaccurate for relativistic case: Objects moving with light’s speed show relativistic effects which were not described by Newton’s law.
- Bending of light: Very strong gravity also bends light which is called gravitational lensing. This phenomenon was also not described by Newton’s law.
- Expansion of Universe: Modern physics shows that the universe is continuously expanding. The dark matter and dark energies are speeding this expansion which was not explained in Newton’s law.
Experimental Validations: The Cavendish Experiment and Beyond
The Cavendish experiment was carried out in 1797-1798 by English scientist Henry Cavendish, which was the first work to measure the force of gravity between masses in a laboratory. Because of different unit systems in use at the time, the gravitational constant does not appear specifically in Cavendish’s works. Instead, he concluded the experiment as Earth’s relative density, or earth’s mass. Although he was the first person to provide accurate results for the parameters.
The apparatus used for the experiment had a torsion balance designed of a 1.8-meter-long wooden rod hanging horizontally from a wire. Lead spheres with two 2-inch-diameters and 1.61-pound were attached to each end. Two large 12-inch, 348-pound lead balls were suspended independently, 8.85 inches apart from the smaller balls. A weak gravitational attraction was detected between the tiny and large balls, which deviated the torsion balance rod by around 0.16″. Thus, it detected the gravitational force for the first time in the lab.
Conclusion
Newton’s law of Universal Gravitation dragged physics towards the next level. We can say, all the advancements in physics like modern physics and Theory of relativity evolved on the basis of Newton’s law. This law is actively studied from basic levels to the higher levels of physics. It gives the precise measurement of weak gravitational forces around us. We can also predict the position of objects after a certain period of time by using Newton’s formula.
Despite some shortcomings like for those with huge masses and speeds, it never fails to explain about our daily activities. Thus, we can find Newton’s law in every aspect like daily instances of walking, playing to the construction of huge structures in engineering. All GPS tracking and satellite launching are possible due to this law. To sum up, it will forever remain as a backbone of physics.
References
Grøn, Ø. (2009). Newton’s Law of Universal Gravitation. In Lecture Notes on the General Theory of Relativity: From Newton’s Attractive Gravity to the Repulsive Gravity of Vacuum Energy (pp. 1-16). New York, NY: Springer New York.
Brill, D. R. and Cohen, J. M. 1966. Rotating masses and their effect on inertial frames, Phys. Rev. 143, 1011–1015.
Harper, W. (2002). Newton’s argument for universal gravitation. The Cambridge Companion to Newton, 174-201.
https://en.wikipedia.org/wiki/Newton%27s_law_of_universal_gravitation
https://www.geeksforgeeks.org/physics/universal-law-of-gravitation/
