A gas’s volume is affected by its amount as well as its temperature and pressure. The Ideal Gas Law is based in part on Avogadro’s Law, a theory proposed by him.

Interesting Science Videos
Avogadro Law Statement
Amedeo Avogadro, an Italian chemist, and scientist, proposed Avogadro’s Law, which states that equal volumes of all gases under identical temperature and pressure circumstances contain an equal number of molecules.
If two distinct gases with the same temperature and pressure occupy the same volume, their number of molecules will be the same. We get the same number of moles of gases if we divide their number of molecules by a set number, (6.023 * 1023), which is the Avogadro number.
number of molecules in gas A = number of molecules in gas B (if V, P, and T are the same).
Where,
- V is Volume of gas
- P is Pressure of gas, and
- T is Temperature
From the mole concept
Number of moles in A = N/Avogadro Number
Number of moles in B = N/Avogadro Number.
We know that the Avogadro number (6.023 1023) is constant.
As a result, the number of moles in A = the number of moles in B = n (assumed).
This means that if the volume of gases remains constant under constant temperature and pressure, the number of moles of gases remains constant. It has been discovered experimentally that any gas at 273K and one atmospheric pressure, i.e., at NTP, has a volume of 22.414 liters (or 22.4 liters). When the volume of a gas at NTP is increased, so is the number of moles of the gas.
As a result, at any fixed temperature and pressure, the volume of a gas is proportional to the amount ‘n’, which is the number of moles in the gas. This is known as Avogadro’s Law.
The mathematical expression of Avogadro’s Law
Avogadro’s law can be represented using the following formula at constant temperature and pressure:
V ∝ n
Chemists use molecule counts to determine the number of atoms and molecules. The number of particles that make up a mole of a substance is known as Avogadro’s number.
In other words, the volume V to the number of gas particles n ratio equals a proportionality constant k.
V/n = k
Avogadro’s law also means the ideal gas constant is the same value for all gases, so:
constant = p1V1/ T1n1 = P2V2/ T2n2
V1/n1 = V2/n2
V1/n2 = V2/n1
Here, p is the pressure of a gas, V is volume, T is temperature, and n is the number of moles.
Derivation Of Avogadro’s Law From The Ideal Gas Law
Boyle’s law and Charle’s law only study the effect of changes in pressure and temperature separately on the volume of gas. This means one of them, either pressure or temperature, must be kept constant to observe the effect on the volume of the given mass of a gas.
The combined gas equation, on the other hand, gives the effect of the simultaneous change of these parameters on the volume of the given mass of gas.
- Let us consider an initial state where V1 is the volume of a certain mass of gas under P1 and T1 conditions of pressure and temperature. Let pressure and temperature be changed to P2 and T2, then the gas reaches a final state where it has volume V2.
Since we have only Boyle’s law or Charle’s law to observe the effect on the volume, let us assume that the changes are brought about by considering an intermediate stage (volume of gas be v) where Boyle’s law is applied on the first step and Charle’s law is applied on the second step as follows:

Now, applying Boyle’s law to the first step,
P1V1 = vP2
v = P1 V1 / P2 ………………….(1)
Similarly, applying Charle’s law to the second step, we get
v / V2 = T1 / T2
v = V2 T1 / T2 …………………….(2)
Equating equations (1) and (2), we get;
P1 V1 / P2 = V2 T1 / T2
P1 V1 / T1 = P2 V2 / T2 ……………………….(3)
Equation (3) is the combined gas equation or ideal gas equation.
The combined gas equation allows us to calculate the volume of a certain mass of gas at any condition of temperature and pressure if the volume of the same mass is given at any other condition of temperature and pressure. This is the importance of this equation.
Combined Gas Equation: Simplified Derivation
The combined gas equation can also be obtained in another form
According to Boyle’s law: V ∝ 1/p when T is constant.
According to Charle’s law: V ∝ T when P is constant.
When both P and T vary at a time, Boyle’s law and Charle’s law are combined
V ∝ T/P
PV = KT ………………..(4)
Since from Avogadro law, V ∝ n at constant P and T, for ‘n’ moles of gas and the proportionality constant of equation (4)
K = nR
PV = nRT ………………….(5)
Equation (5) is called ideal gas equation that can be used to figure out Avogadro’s law.
Graphical Representation of Avogadro’s Law
The following is a graphical illustration of Avogadro’s law (with the amount of substance on the X-axis and the volume on the Y-axis):
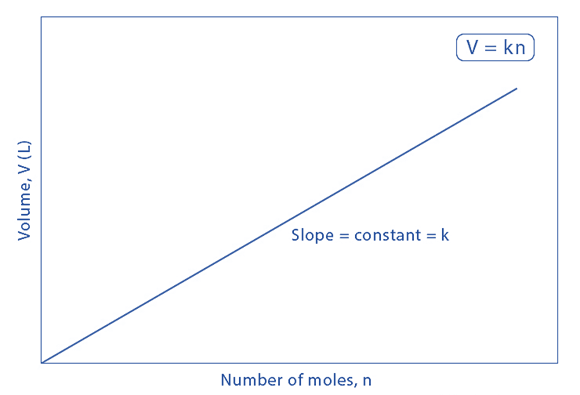
Graphical Representation of Avogadro’s Law
Applications of Avogadro’s Law
- This law helps us to determines the atomicity of the gas.
- We can derive the molecular formula of a gas.
- Avogadro’s law helps us to determine the relation between molecular weight and vapour density.
- We can also explain the Gay-Lussac’s law employing this law.
- Determines the relationship between gram molecular weight and gram molecular volume.
Limitation of Avogadro’s Law
- Avogadro’s law does not apply to liquids or solids. It is only applicable to gas.
- The law is not valid for very dense or very light gases.
- Avogadro’s Law is not applicable for very hot and cold gases.
Examples of Avogadro’s Law
- Breathing demonstrates Avogadro’s Law. When humans breathe in, their lungs expand and more air enters the lungs.
- Avogadro’s rule is also used for deflating car tires. When air comes out of a tire, the amount of air molecules in the tire decreases. The gas takes up less space. It was resulting in the tire losing its shape and deflating as a result.
- A bicycle pump demonstrates Avogadro’s law. The pump takes air from outside and puts it into something that is not inflated. When there are more gas molecules, the shape of the object changes.
- A soccer ball has a hard outer layer and an inner bladder. When the ball loses air, it becomes flat and the inside part also becomes flat. It makes the ball unable to bounce. You can use an air pump to increase the amount of air in the bladder. The more air molecules there are in a certain volume, the greater the number of air molecules in that volume. Pumping air into a soccer ball demonstrates Avogadro’s Law.
What is Avogadro’s Number?
The number of particles in 1 mole (or mol) of a substance is known as Avogadro’s number. These particles can be atoms, molecules, or electrons. Approximately 6.022140857×1023 mol−1 is the value of Avogadro’s number.
Avogadro’s number was not discovered by Amedeo Avogadro. Physicist Jean Baptiste Perrin named the constant Avogadro’s number in 1909.
Numerical Problem Related to Avogadro’s Law
0.8 moles of a gas are present in a 7.0 L sample at 300 oC and 2.00 atm of pressure. If you add 0.30 moles of gas at the same pressure and temperature, what will be the final total volume of the gas?
Solution:
Avogadro’s Law formula.
Vini=Vfnf
Where;
- Vi = initial volume
- ni = initial number of moles
- Vf= final volume
- nf = final number of moles
The initial volume is 7.0 liters and the initial amount is 0.8 moles. When 0.30 moles are added:
nf= ni +0.30
nf= 1.1 mole
Now, Vf = Vi nf/ni
Vf =(7.0L ✕ 1.1mole) / 0.8 mole
Vf =7.7L / 0.8
Vf = 9.625 L
As a result, the final volume of the gas is 9.625 liters.
In a 2.5 L container, 40 g of nitrogen gas is stored. The pressure exerted by the gas on the container is 2 atm. What is the final quantity of gas in grams in the container if gas is added until the volume reaches 4.0 L if the pressure remains constant?
Solution:
Given
Mass of nitrogen = 40 g
n1 = Mass/Molar mass = 40 g / 28 gM-1 = 1.43 M
V1 = 2.5 L
V2 = 4 L
From Avogadro’s law,
V1/n1 = V2/n2
n2 = n1 x V2/V1
n2 = 1.43 M x 4 L /2.5 L
n2 = 2.29 M
Thus, amount of nitrogen
= 2.29 M x 28 gM-1 = 64 g
Frequently Asked Questions (FAQ)
What does Avogadro’s law state?
Avogadro’s Law states that when the temperature and pressure stay the same, two gases with the same volume will have the same number of molecules.
Avogadro’s Law: V1/n1=V2/n2
What is the formula of Avogadro’s law?
The formula for Avogadro’s law is:
V ∝ n or V/n = k
The formula for calculating the volume of a gas involves three variables: “V” for volume, “n” for the amount of gas (measured in moles), and “k” which is a proportionality constant for given pressure and temperature.
Video on Avogadro’s Law
References
- https://www.britannica.com/science/Avogadros-law
- https://www.thoughtco.com/definition-of-avogadros-law-605825
- https://www.expii.com/t/avogadros-law-overview-formula-8157
- https://www.chemteam.info/GasLaw/Gas-Avogadro.html
- Helmenstine, Anne Marie, Ph.D. “What Is Avogadro’s Law? Definition and Example.” ThoughtCo, Aug. 25, 2020, thoughtco.com/definition-of-avogadros-law-605825.
- https://www.geeksforgeeks.org/gas-laws-statements-types-applications/
- https://www.chemistrylearner.com/avogadros-law.html

