In any compound, intermolecular forces of attraction and thermal force operate in opposite directions. The intermolecular force of attraction tends to keep the particles together while the thermal force tends to keep the particles apart. The extent of these forces results in states of matter such as solid, liquid, and gas.
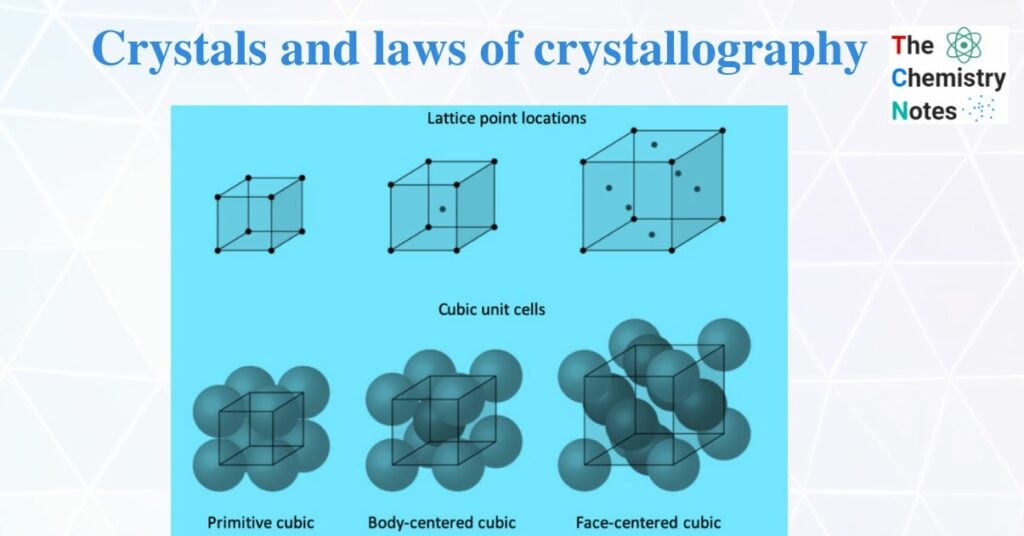
Crystalline solids are pure solid substances that consist of atoms, ions, or molecules arranged in a definite pattern with fixed geometric shapes. They have a sharp melting point. When minute crystals are packed together in well-defined order then a crystalline solid is formed. The position of each constituent particle in a three-dimensional structure of a crystal is represented by a point which is called a lattice point. The regular arrangement of an infinite set of lattice points in space is a lattice or space lattice.
Interesting Science Videos
Unit cell
It is a structural unit of the crystal. The smallest repeating unit from which crystal lattice is formed is known as a unit cell. These unit cells are repeated in a three-dimensional pattern to give a large crystal. A unit cell also represents the characteristic feature of the entire crystal.
In the three-dimensional structure, the unit cell is characterized by :
1. Its dimensions along three edges a, b, and c. These edges may or may not be mutually perpendicular.
2. The angle between two edges α (angle formed between two edges a and b), β (angle formed between two edges b and c), and γ (angle formed between two edges c and a).
Types of unit cells
Based on the arrangement of the constituent particle in the crystal unit cells are broadly classified into two groups. They are as follows:
1. Simple or primitive cell
2. Centered unit cell or non-primitive unit cell
Simple or primitive cell
In this cell, the constituent particles (atoms, ions, or molecules) are present in each corner. For example, polonium has a primitive cubic unit cell.
Centered unit cell or non-primitive unit cell
In this arrangement, constituent particles are present at the center of the face or body along with corner. It is further classified into three types. They are;
a. Body-centered cubic unit cell (BCC)
A body-centered cubic unit contains atoms at all corners of the unit cell and the center of the body of the unit cell. For example, potassium has a body-centered cubic unit cell.
b. Face-centered cubic unit cell
The face-centered cubic unit cell has atoms at each corner of the unit cell and also at the center of each face. For example, copper has a face-centered cubic unit cell.
c. End centered unit cell
In this type of unit cell, the constituent particles are present at the corner of two opposite faces of elongated sides in addition to each corner of the unit cell.
Types of crystal lattices
1. Bravais lattice
2. Non- bravais lattice
In the Bravais lattice, all lattice points are equivalent, so all atoms in the crystal must be of the same kind. While in non- bravais lattice some of the lattice points are nonequivalent. They are also referred to as a lattice with a basis. A basis is a group of atoms located near each site of a Bravais lattice.
Crystal system
The unit cells are characterized by their edge lengths and interfacial angles. These are also called as unit cell parameters. On the basis of these parameters, there are seven classes of the unit cell. This is also called the seven-crystal system.
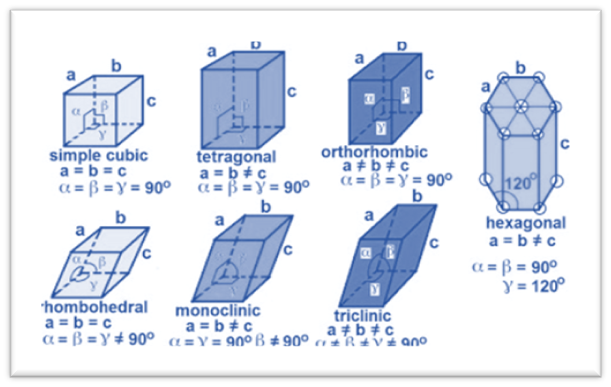
Cubic
This is a lattice system in which all three angles have the same length and are at right angles to each other.
Tetragonal
In this system, only the main axis have different dimension while the other two are the same in length.
Orthorhombic
This type of crystal lattice structure consists of three perpendicular axes, but the lengths of these axes vary.
Monoclinic
In this crystal system, two axes are perpendicular, while the third is inclined to form a different angle. These axes have different lengths.
Triclinic
All three axes in this system are inclined to one another and have the same length.
Rhombohedral
In this crystal system, two axes are perpendicular, while the third is inclined to form a different angle. These axes also have same lengths.
Hexagonal
This type of crystal lattice structure consists of two perpendicular axes while the third is inclined at a different angle.
Overview of crystal systems
| S.N | Name of crystal system | Edge length | Interfacial angle | Examples |
| 1. | Cubic | a = b = c | α = β = γ = 90o | NaCl, KCl, ZnS, Diamonds, Pb, Ag, Au |
| 2. | Tetragonal | a = b ≠ c | α = β = γ = 90o | TiO2, White tin, Zircon, NiSO4, CaSO4 |
| 3. | Orthorhombic or Rhombic | a ≠ b ≠ c | α = β = γ = 90o | KNO3, K2SO4, PbCO3, BaSO4, MgSO4, Rhombic sulphur |
| 4. | Monoclinic | a ≠ b ≠ c | α = γ = 90o, β ≠ 90o | Na2SO4. 10H2O, Ca2SO4. 2H2O, FeSO4. 7H2O, Monoclinic sulphur |
| 5. | Triclinic | a ≠ b ≠ c | α ≠ β ≠ γ ≠ 90o | CuSO4. 5H2O, K2Cr2O7, H3BO3 |
| 6. | Rhombohedral or Trigonal | a = b = c | α = β = γ ≠ 90o | NaNO3, CaSO4, MgO, Quartz, As, Sb, Bi, KMnO4 |
| 7. | Hexagonal | a = b ≠ c | α = β = 90o , γ = 120o | ZnO, Graphite, Ice, CDS, HgS |
Laws of crystallography
Crystals are solid homogeneous substances with sharp melting points bounded by plane faces meeting at a sharp edge where constituent particles are arranged in a definite recurring geometric pattern.
Crystallography is the branch of science that deals with the arrangement and bonding of atoms in crystalline solids, as well as the geometric structure of crystal lattices. Crystallography is based on three fundamental laws which are also known as laws of crystallography. These are as follows:
1. Law of constancy of interfacial angle
2. Law of constancy of symmetry
3. Law of rational indices
Law of constancy of interfacial angle
Under different conditions, the size of faces or shape of crystals may be different but the interfacial angle between corresponding faces remains the same. The law of interfacial angle states that under the same physical condition the angle between the corresponding faces on various crystals of the same substance is constant. This law was developed by Steno in 1669 performing a series of experiments. This is also known as Steno’s law.
Law of constancy of symmetry
According to this law, all crystals of a substance have the same symmetry elements which are the plane of symmetry, the axis of symmetry, and also the centre of symmetry.
Centre of symmetry
It is an imaginary point within the crystal that intersects the opposite faces of the crystal at an equal distance. A crystal can only have one centre of symmetry. Some of the crystals may not consist centre of symmetry.
Axis of symmetry
It is an imaginary line passing through the crystal so that exactly a similar appearance occurs more than once in one complete revolution of 360o when the crystal is rotated about this line.
Plane of symmetry
It is defined as an imaginary plane passing through the centre of a crystal that divides the crystal into two halves so that one half is the mirror image of the other half.
Law of rational indices (Hauy’s Law)
The Law of constancy of interfacial angle states that the structure of a crystal can be determined from the study of external forms. But in 1784 Abbe Rene Hauy suggested that the regular external form of crystal is the consequence of inner regularities in the arrangement. Unit cells are building units of a crystalline substance. Such unit cells can be defined in terms of three crystallographic axes. The planes of crystal are also expressed in terms of three crystallographic axes.
This law states that the ratio of intercepts of the different faces of a crystal with the three axes is constant and can be expressed by the rational numbers that the intercepts of any face of the crystal along the crystallographic axes are either equal to unit intercepts (that is, intercepts made by the unit cell) a, b, c or various simple whole number multiples of them such as na, n1 b, n2c, where n, n1, and n3 are called as Weiss indices.
1. Weiss indices are crystal parameters and are also used to represent the plane of a crystal
2. Weiss indices are usually the whole number but they may be fractional or infinity.
Miller indices
Besides the Wiess indices the Miller indices method, developed by Miller in 1839, can represent the plane of a crystal in terms of crystallographic axes and axial ratio.
If planes are parallel to the crystallographic axes then infinity is used in Weiss indices which are rather difficult to calculate. So Weiss indices are replaced by Miller indices.
Miller indices may be defined as the reciprocal of coefficient of intercept made by unit plane which is expressed as integers. The orientation of the lattice plane is described by its Miller indices. Miller indices of a plane of a crystal are inversely proportional to the intercepts made by the face on crystallographic axes that are commonly represented by the letters h,k, and l.
h = a/ Intercept of a plane along the X-axis
k = b/ Intercept of a plane along the Y-axis
l = c/ Intercept of a plane along the Z-axis
So, from this, it can be concluded that
a) The higher the intercept value, the lower the miller indices value.
b) When a plane is parallel to the axes, it cuts the axes at infinity, so Miller indices is zero.
c) If a face’s intercept is negative, i.e., the face cuts the axis when extended in the opposite direction, Weiss indices have negative values. A bar is placed over the Miller indices value to write it.
References
- West A. R. (2014). Solid state chemistry and its applications (Second edition student). John Wiley & Sons.
- https://unlcms.unl.edu/cas/physics/tsymbal/teaching/SSP-927/Section%2001_Crystal%20Structure.pdf
- https://www.vedantu.com/chemistry/crystal-structure
- https://byjus.com/chemistry/bcc-fcc-primitive-cubic-unit-cell/
- http://epgp.inflibnet.ac.in/epgpdata/uploads/epgp_content/S000448GO/P000595/M022495/ET/1505370994E-TextLawsofCrystallographyandCrystalSystem.pdf
- https://old.amu.ac.in/emp/studym/100002812.pdf
- https://www.britannica.com/science/crystallography
- https://wisc.pb.unizin.org/minimisgenchem/chapter/types-of-unit-cells-body-centered-cubic-and-face-centered-cubic-m11q5/
