Stress and strain are common terms in the field of engineering and material science. Stress is the amount of force per unit area that is applied to a material. It is a material’s fundamental resistance to deformation in the presence of an external load. Pascals (Pa) or pounds per square inch (psi) are two common measurements of force per unit area used to quantify stress. However, strain refers to the deformation or shape change that a substance undergoes in reaction to stress. It measures the amount of deformation a material experiences under stress and is often given as a decimal fraction or a percentage. The strain has no dimensions.

In general words, stress is the amount of force per unit area that is applied to a material, whereas strain is the deformation or change in shape that the applied force causes in the material. Strain is the material’s reaction to the stress that is applied to it. A stress-strain curve, which illustrates the behavior of the material under various stress levels, is frequently used to illustrate the relationship between stress and strain for a certain material. This curve can give important details on the characteristics of the material, like its ultimate strength, yield strength, and elasticity.
Interesting Science Videos
What is Stress?
- The force per unit area acting on a substance is called stress. This characteristic helps in defining the behavior of various materials under particular loading circumstances.
- A material generates internal forces to withstand deformation when an external force is applied to it. This internal resistance is quantified by stress, which is commonly expressed in Pascals (Pa) or pounds per square inch (psi), units of force per unit area.
- Simply, stress indicates the amount of force applied to a certain location within a material.
- Stress is a widely used term for engineers and materials scientists as it helps in anticipating the behavior of materials under external stresses, facilitating the creation of safe, dependable, and effective structures and components.
An object can experience a variety of stresses inside it, such as torsional, shear, compressive, and tensile stresses. Each type of stress is represented by a different symbol, the main one being the Greek letter sigma (𝜎). The following is the mathematical expression for stress:
𝜎 = F/A
Where,
σ is stress, measured in N/m² or Pa
A is the cross-sectional area to which the force is applied, measured in m²
F is the applied force, measured in Newtons (N)
- Stress is a material’s response to an external force. In order to help us choose the best material for a given application, we can define the observed stress under specific, well-defined test circumstances (for example, yield strength is usually described as the stress recorded at 0.2% strain).
- When analyzing the impact of stress, stress testing, and stress analysis are two factors that are crucial:
- Stress analysis is the process of using the knowledge gained from stress testing to choose the best material or alter a design for maximum strength or durability (or, at the very least, to meet the requirements of the application).
- Stress testing is the process of applying various forces to an object to see how the object will react under different loading conditions.
- These techniques are primarily intended to determine if a material is able to sustain the forces it will encounter in practical applications or to identify any weak points in a particular design. This is particularly helpful in the construction sector, where concrete constructions, for instance, need to be able to bear a variety of forces without collapsing.
- Numerous other parameters, including the elastic modulus, yield strength, ultimate strength, and fracture toughness of a material, can also be calculated or ascertained using stress. This gives us further information about a material which may help in the material selection phase.
Types of Stress
- Tensile Stress: When a material is pushed or stretched, it experiences tensile stress and elongates in the direction of the applied force. It’s the same kind of tension that a rope feels when you tug on both ends of it. The calculation of tensile stress involves dividing the applied force by the material’s cross-sectional area.
- Compressive stress: When a material is compressed or pushed, it shortens along the direction of the applied force, leading to the formation of compressive stress. It is the reverse of tensile stress and is typically felt by pillars or columns that are subjected to a downward load. Another method for calculating compressive stress is to divide the force exerted by the cross-sectional area.
- Shear stress: When forces are applied parallel to a material’s surface, shear stress results, causing the material to slide or shear. It feels similar to rubbing your hands together firmly, applying shear stress to the skin. By dividing the force applied parallel to the surface by the cross-sectional area, shear stress is computed.
- Torsional Stress: When a material is twisted around its longitudinal axis, torsional stress results. It frequently occurs in constructions susceptible to torque, such as shafts or springs. The torsion formula, which takes into account the applied torque, the polar moment of inertia, and the shaft’s radius, is used to compute torsional stress.
- Bearing Stress: When a force is exerted over a small area, such as the contact between two components, bearing stress arises. Essentially, it is the force divided by the applied area. In structural design, bearing stress is particularly important in joints and connections where components come into contact.
How Is Material Stress Calculated?
- Since it is impossible to quantify stress directly, we must either measure the applied forces or the consequent deformations. Understanding the link between the applied forces (strains) and the resulting deformations (strains) is essential to measuring deformation.
- An indirect method of measuring the amount of stress generated by applied forces is to employ experimental testing procedures and instruments such strain gauges, extensometers, piezoelectric materials, load cells, ultrasonic testing, x-ray diffraction, and photoelasticity.
- Stress can be calculated using the stress equation (σ=F/A) once the force’s magnitude has been determined or measured.
- Stress analysis is a useful tool to determine the possible consequences of different forces on an object. It can be carried out in a number of ways, including computational simulations, analytical mathematical modeling, experimental testing, and combinations of these approaches. The material being tested, the kind of stress being measured, and the required degree of precision all influence the procedure selection.
Application of Stress
- In a variety of areas, including materials, mechanical, aerospace, and civil engineering, stress analysis is essential to engineering design. Stress analysis is a tool used by engineers to make sure materials, components, and structures can survive the forces applied to them while they are in use. Stress distributions can be computed and analyzed by engineers to optimize designs for durability, efficiency, and safety.
- By evaluating how various materials react to outside forces, stress analysis helps in material selection. Engineers select materials for particular purposes based on a variety of criteria, including fatigue resistance, ductility, stiffness, and strength. Engineers can guarantee that structures and component parts operate dependably for the duration of their intended lives by choosing materials with the right qualities.
- Stress analysis is essential to structural engineering design of buildings, bridges, dams, and other infrastructure. Engineers evaluate the effects of various loads on structures, including live, dead, wind, and seismic loads. Engineers can design structures that withstand deformation, cracking, or collapse under a range of loading circumstances by comprehending stress distributions.
- Stress testing is done to confirm a product’s functionality and safety in real-world settings. To evaluate a product’s endurance and structural integrity, engineers model loads such as mechanical, thermal, and environmental stressors. Engineers can make incremental changes and optimizations by using testing to find probable failure sources and design defects.
- In manufacturing processes, stress analysis is utilized to ensure the integrity and quality of the final product. Engineers examine deformation and stress concentrations that occur during the forming, welding, and assembling operations. Cracks, fractures, and dimensional inaccuracies can be prevented by engineers by streamlining manufacturing processes and decreasing stress concentrations.
- In sectors like the automobile, aerospace, nuclear, and oil and gas industries, stress analysis is essential to safety and risk assessment. In order to assess the structural integrity of crucial parts like pressure vessels, pipelines, aircraft wings, and vehicle frames, engineers use stress analysis. Engineers are able to analyze failure probability and identify possible failure modes in order to reduce risks and guarantee that regulations are followed.
- Innovation and progress in materials science and engineering are driven by stress analysis. Researchers investigate cutting-edge manufacturing processes, composite constructions, and new materials to boost sustainability, reduce weight, and increase performance. Researchers help to build safer, more effective, and more resilient technology by pushing the frontiers of materials and design principles.
In order to make sure that structures like buildings, bridges, and airplanes can resist the pressures they will be subjected to, stress analysis is crucial during the design and testing phases. Selecting the right material for a given application is made easier by knowledge of the stress behavior of various materials. By determining the reason for material failure, stress analysis can assist in improving manufacturing and design procedures. Stress measurement is a useful tool for ensuring material quality and consistency, particularly in manufacturing operations where accuracy is essential. Understanding stress can assist avoid material and structural breakdowns, which can have serious safety repercussions.
What is Strain?
- Strain is defined as the ratio of the change in size or shape of a material to its original size or shape.
- Strain is a measure of the deformation of a material under the influence of an external force. This indicates the degree of distortion that a material experiences when stressed.
Mathematically, strain can be calculated using the formula:
ε = (L – L0) / L0
Where,
Strain (ε) is the fractional or percentage change in length or another dimension.
L is the length of the material after an external load is applied
L0 is its original length measured in the same units as “L”
- The definition of strain is the ratio of a material’s changed length (or other dimension) to its initial length (or dimension). Strain can be stated as a percentage or as a unitless quantity.
- Strain can be measured in a number of ways. Extensometers and strain gauges are the most widely used techniques. These two directed procedures necessitate contact between the instrument and the specimen. Piezoelectric sensors, acoustic emission sensors, and digital image correlation (DIC) are additional techniques that can be applied.
- A material will distort when an external force is applied to it; this deformation is quantified as strain. The kind of material, its composition, the amount, direction, and kind of applied stresses, among other variables, all affect how the material will deform under stress.
- Since strain offers a means of measuring and comprehending how a material deforms under stress, it is a crucial feature of materials. Engineers can compute crucial parameters required for application design when stress and strain data are obtained concurrently, as in the case of the stress-strain curve produced during a basic tensile test. Strength, toughness, elasticity, strain energy, yield point, elongation under load, and resilience are a few of these mechanical characteristics.
Types of Strain
Tensile, shear, compressive, volumetric, and thermal strains are the names for the different types of stress that are applied, and these names correspond to the strains that are detected. When a material is stretched or elongated, it experiences tensile strain; when it is compressed or shortened, it experiences compressive strain. Stress applied in a direction parallel to the cross-section of interest results in a shear strain. Volumetric strain is the term used to describe changes in a material’s volume as a result of alterations in its size or shape. Finally, a material’s change in length or volume as a result of temperature fluctuations is referred to as thermal strain.
- Linear strain: When a material is subjected to tensile or compressive stress, it can deform along a specific direction. This phenomenon is referred to as linear strain, also known as axial strain. It is computed by dividing the length change by the material’s initial length. A material experiences positive linear strain while stretching (tensile stress) and negative linear strain during compression (compressive stress). In structural engineering, linear strain is a basic concept that is used to evaluate the elongation or contraction of materials under stress.
- Shear strain: Shear strain occurs when shear stress causes neighboring layers of a material to slip past one another. It is the shift in angle between the material’s initially perpendicular lines. Applications involving cutting, bending, or torsional loading frequently result in shear strain. In disciplines like mechanical engineering, where shear strain affects the design and analysis of components subjected to shearing pressures, an understanding of it is crucial.
- Volumetric strain: The term “volumetric strain” refers to a material’s change in volume under hydrostatic or pressure stress. It is the proportion of the material’s original volume to its changed volume. Changes in the material’s three dimensions—length, width, and height—are taken into consideration by volumetric strain. This kind of strain is important in materials science because it helps explain how materials contract or expand, and in geotechnical engineering, it is used to examine how soil and rock behave under pressure.
How Does a Strain in Materials Work?
A material will distort when an external force is applied to it; this deformation is defined as strain. The kind of material, its composition, the amount, direction, and kind of applied stresses, among other variables, all affect how the material will deform under stress. Under stress, materials can generally deform in three primary ways:
- Elastic Deformation: This is the deformation that takes place in a material when it is stressed and then returns to its original shape when the stress is released. Stated differently, the material is capable of withstanding a specific degree of stress without experiencing irreversible deformation.
- Plastic Deformation: When a material is stressed beyond its elastic limit, plastic deformation sets place, resulting in permanent distortion. Even after the tension is released, the material experiences an irreversible change in shape. Ductility is the measure of how much plastic deformation a material can withstand before breaking.
- Fracture: When the material’s strength is exceeded by the applied stress, the material breaks or fails. A material’s strength is an indicator of how much stress it can bear before breaking or deforming plastically.
Application of Strain
- In order to evaluate the integrity and performance of engineering structures, including buildings, bridges, dams, and aerospace components, strain measurement is crucial to structural analysis. Through strain monitoring, engineers may pinpoint regions of elevated stress concentration, deformation, or possible failure, enabling them to enhance designs and guarantee structural stability.
- Strain measurement is used in geotechnical engineering to examine how rocks, soils, and other geological materials behave under different loading scenarios. Engineers can evaluate elements like settlement, deformation, stability, and bearing capacity by measuring strains in the ground or within structural foundations. This information is useful for designing and constructing infrastructure projects like buildings, roads, and retaining walls.
- In materials testing, strain measurement is frequently used to describe the mechanical characteristics of materials such metals, polymers, ceramics, and composites. Engineers can ascertain critical parameters for material selection and design, such as tensile strength, compressive strength, modulus of elasticity, and ductility, by putting materials to controlled loading conditions and monitoring strain responses.
- In manufacturing operations including metal forming, welding, machining, and additive manufacturing, strain measurement is essential. Engineers can verify product quality and dimensional accuracy, improve process parameters, identify anomalies or flaws, and prevent premature component failure by keeping an eye on stresses during production processes.
- Strain measurement is a tool used in biomechanics and biomedical engineering to investigate the mechanical characteristics of biological tissues and structures, including muscles, tendons, ligaments, and bones. Researchers can diagnose and treat musculoskeletal injuries and diseases as well as gain insight into the biomechanics of human movement by measuring stresses experienced during common activities like walking, running, and leaping.
- In environmental monitoring applications, strain measurement is also used to investigate natural events like landslides, earthquakes, and glacier movements. Researchers can monitor tectonic activity, forecast seismic risks, and evaluate the stability of slopes and ice masses by measuring stresses in the Earth’s crust or within geological formations. This helps to reduce the risk of disasters and manage geohazards.
- Structural health monitoring (SHM) involves the installation of strain sensors on engineering structures in order to continually monitor and evaluate the structures’ integrity, performance, and condition over time. SHM systems can recognize fatigue, corrosion, structural damage, and other degradation mechanisms by sensing changes in strain patterns or levels. This allows for rapid maintenance, repair, or retrofitting to avert catastrophic failures.
Stress vs Strain
| Property | Stress | Strain |
| Definition | Stress is the amount of force per unit area that is applied to a material. | Strain refers to the deformation or shape change that a substance undergoes in reaction to stress. |
| Formula | σ=F/A | ε=L-L0/L0 |
| Units | Pa (N/m2) or psi | Dimensionless or % |
| Cause | External force | Deformation caused by stress |
| Physical traits | A material may compress, stretch, twist, or alter form as a result of stress. | The alteration in a material’s dimensions brought about by the application of force. Both elastic and plastic strains are possible. |
| Effect | Affects a material’s strength, stiffness, and other mechanical qualities, and causes it to deform or change shape. An excessive amount of stress may cause the material to permanently distort or even fracture. Over time, materials may suffer from fatigue, corrosion, and other types of degradation. | The alteration in a material’s dimensions is brought about by the application of force. Both elastic and plastic strains are possible. |
Stress-Strain Curve
An illustration of the relationship between stress and strain in a material is called a stress-strain curve. It is produced by measuring the equivalent strain that a material experiences after being exposed to progressively higher stress levels in a sample of the material.
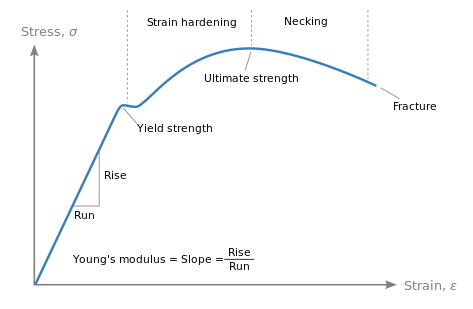
- Stress-strain diagrams are frequently used to examine a material’s behavior from loading to failure.
- Design engineers can utilize the distinct stress-strain patterns shown by various materials to determine critical mechanical attributes such as resilience, ductility, yield point, toughness, elasticity, and strain energy. This is essential for determining the forces necessary to cause plastic deformation, which is useful when developing applications and carrying out processes like extrusion, rolling, and bending.
- The elastic region and the plastic region are the two main components of the stress-strain curve. The material deforms in the elastic area in reaction to applied stress, but the distortion is not irreversible. Releasing the material from its stress causes it to revert to its initial dimensions. In this area, stress and strain have a linear connection; the slope of the line is known as the material’s elastic modulus or Young’s modulus.
- When a material is in the plastic area, it deforms permanently in reaction to applied stress; that is, it does not recover when the stress is released. In this area, stress and strain have a nonlinear connection. It is dependent upon the material’s characteristics, including its ductility, yield strength, and ultimate strength.
References
- https://www.tutoroot.com/blog/stress-and-strain-definition-stress-strain-curve/
- https://www.linearmotiontips.com/mechanical-properties-of-materials-stress-and-strain/
- https://www.toppr.com/guides/physics/mechanical-properties-of-solids/stress-and-strain/
- https://www.xometry.com/resources/materials/stress-vs-strain/#:~:text=Stress%20refers%20to%20the%20force,strain%20is%20not%20always%20straightforward.
