The concepts of Gibbs free energy and equilibrium constant are fundamental principles within the realm of thermodynamics. Equilibrium is attained in a system when the rates of the forward and reverse reactions are equivalent. In this particular instance, it can be observed that neither of the reactions under consideration exhibit spontaneity. We will learn about the correlation between Free energy and Equilibrium, as well as the equilibrium constant in this article.
Interesting Science Videos
Gibbs Free Energy
The concept of Gibbs free energy, also known as free energy, refers to the measure of the energy that is readily available in a given system to do work. The equation representing a change in free energy (ΔG) is as follows:
Δ G = Δ H − T Δ S
Where:
- ΔH = change in enthalpy
- ΔS = change in entropy,
- T = temperature.
- If G is positive, the reaction is not spontaneous because energy had to be given to the system. In other words, unless additional energy is provided, the reaction cannot occur.
- If Δ G is negative, that means that energy was consumed by the system, so the reaction is spontaneous. This means that the system doesn’t need more energy for the reaction to happen.
Chemical Equilibrium
Consider a reversible reaction taking place at constant temperature:
A + B ⇌ C + D
Where, Reactants A and B undergo a chemical reaction to yield products C and D.
The reactants or products are “favored” in an equilibrium state. Consequently, there will be a higher level of either substance. We measure the difference with the equilibrium constant.
The (equilibrium constant) Keq, which represents the ratio of the concentrations of products to reactants at equilibrium, serves as an indicator of the direction in which the chemical reaction is favored. The equation represents the constant K for a reaction.
a A + b B ⇌ c C + d D
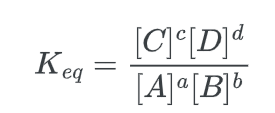
Where the large brackets indicate “concentration of” and a, b, c d are the stoichiometric coefficients for each species.
- If Keq < 1, then the reactants are favored
- If Keq > 1, then the products are favored
Relating Gibbs Free Energy and Equilibrium constant
The concepts of Gibbs free energy and equilibrium constant are fundamental principles within the realm of thermodynamics.
The determination of the ΔG value for a given chemical reaction provides insight into the thermodynamic favorability of the system towards either the reactants or products at the point of equilibrium. It is known that the equilibrium constant, Keq, establishes a relationship between the concentrations of all substances involved in the reaction when it reaches equilibrium. It is reasonable to assume that there exists a correlation between the ΔG° values and Keq. A more sophisticated analysis of thermodynamics results in the derivation of the subsequent equation:
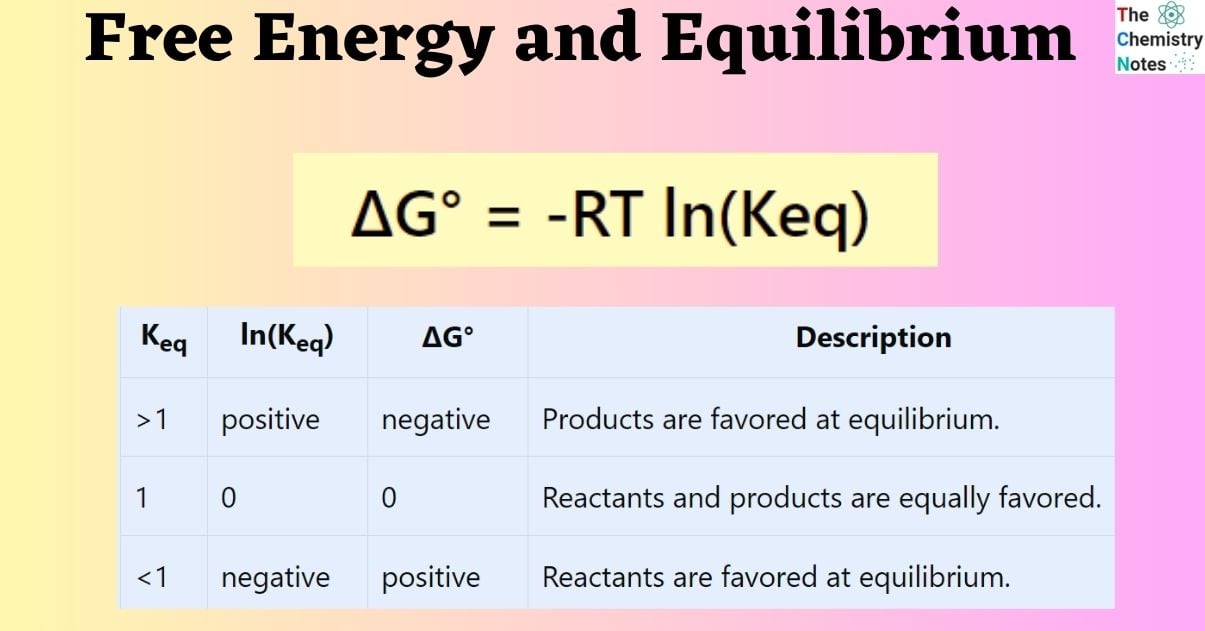
ΔG° = -RT ln(Keq)
In this context, R denotes the ideal gas constant with a value of 8.314 J/K•mol. The variable T represents the temperature in Kelvin, while ln(Keq) signifies the natural logarithm of the equilibrium constant.
In instances where Keq is significant, the reaction products are given preference, thereby indicating a negative ΔG°. In cases where Keq is small, the reactants are considered to be the preferred species. It can be observed that the logarithm of a value below unity in the natural base is negative. Consequently, in cases where the equilibrium constant (Keq) is less than one, the standard change in Gibbs free energy (ΔG°) exhibits a positive sign.
The following table presents a summary of the correlation between ΔG° and Keq.
| Keq | ln(Keq) | ΔG° | Description |
|---|---|---|---|
| >1 | positive | negative | Products are favored at equilibrium. |
| 1 | 0 | 0 | Reactants and products are equally favored. |
| <1 | negative | positive | Reactants are favored at equilibrium. |
Derivation of relation between Gibbs free energy and equilibrium constant
The value of ΔG° can be utilized to determine Keq, and conversely, Keq can be calculated using ΔG°. For starters, it is important to have a clear understanding of the reaction quotient.
The reaction quotient (Q) represents the ratio of products to reactants that are not in a state of equilibrium.
For a general equation;
A + B → C + D
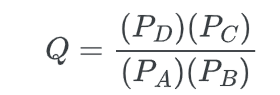
Where P is the partial pressure of the species. At equilibrium, Q=Keq.
To establish our equation, it is necessary to assume that the reaction is taking place in the gaseous state. The free energy change of species A can be expressed as:
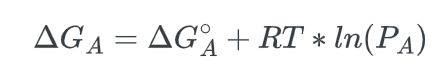
Where R is the gas constant, T is the temperature and the symbol for the natural logarithm is, ln. Given this equation, we can solve for the change in the free energy of the overall process, ΔG:
- First we note that the standard free energy change is given by:
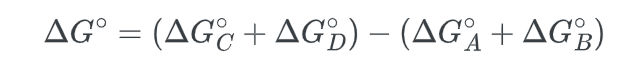
- Next, we calculate the change in free energy for the overall process:
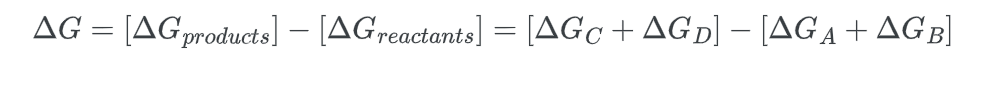
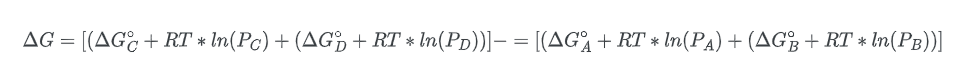
Rearranging the equation;
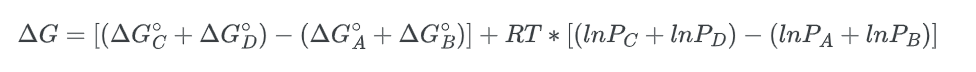
Substituting the value, we get;
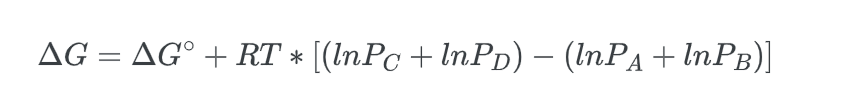
combining the natural logarithms, we get:
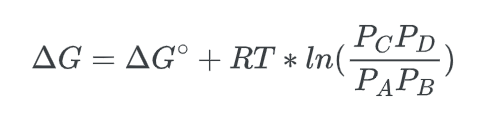
we can substitute in the reaction quotient to get:
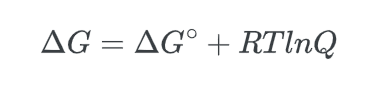
- Lastly, we know that at equilibrium, Q = Keq, and that, ΔG, the non-standard free energy difference is equal to zero, ΔG = 0, thus:
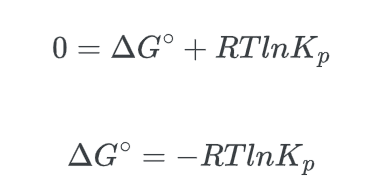
The “P” is used to denote that Keq is being measured in terms of pressures. This equation remains valid for other forms of K, such as Kc (which is expressed in terms of concentration).
Calculation of Gibbs Free Energy and the Equilibrium Constant
The formation of nitrogen monoxide from nitrogen and oxygen gases is a reaction that strongly favors the reactants at 25°C.
N2(g) + O2(g) 2NO(g)
The actual concentrations of each gas would be difficult to measure, and so the Keq for the reaction can more easily be calculated from the ΔG°, which is equal to 173.4 kJ/mol.
Given:
- ΔG° = +173.4 kJ/mol
- R = 8.314 J/K•mol
- T = 25°C = 298 K
- Keq = ?
ΔG° = -RT ln(Keq)
ΔG° = -(8.314 J/K•mol)(298 K) ln(1.4 × 10-8)
= 45,000 J/mol
= 45 kJ/mol
The significant increase in free energy results in an extremely low Keq value. Both pieces of evidence suggest that the reactants are strongly favored, resulting in a minimal amount of product molecules present at equilibrium.
Frequently Asked Questions (FAQ)
What is the relationship between free energy and equilibrium constant?
There exists an inverse relationship between the equilibrium constant (K) and the free energy change (ΔG). The equation relating to two is: K=e(ΔG*/(RT)) Where R is the gas constant and T is temperature.
Is Gibbs free energy zero at equilibrium?
Yes, the change in free energy is 0 at equilibrium.
What is the concept of free energy?
The term “Free Energy” pertains to the energy present in a system that can be utilized to perform work. This energy is calculated by subtracting any energy that cannot be used to perform work from the system’s internal energy.
References
- https://www.studysmarter.co.uk/explanations/chemistry/physical-chemistry/free-energy-and-equilibrium/
- https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Thermodynamics/Fundamentals_of_Thermodynamics/Free_Energy_and_Equilibrium
- https://www.inspiritvr.com/general-chemistry/entropy-and-free-energy/free-energy-and-equilibrium-constant-study-guide
- https://georgiasouthern.libguides.com/c.php?g=943952&p=6804634
- https://www.ck12.org/book/ck-12-chemistry-intermediate/section/20.3/
- https://www.jove.com/science-education/11431/free-energy-and-equilibrium
- https://general.chemistrysteps.com/gibbs-free-energy-and-equilibrium-constant/
