Lattice energy is the term used to describe the type of energy that is released whenever ions with opposing charges join together to create a crystalline lattice. In order to describe the stability of ionic solids, the concept of Lattice Energy is utilized. The crystalline structure makes it possible for each ion to interact with several ions that have opposing charges. This results in a change in the enthalpy of the system that is extremely beneficial. As a result of their interaction, ions with opposing charges give out a significant amount of energy. Ionic solids are characterized by having extremely high melting and boiling points due to this property.
Interesting Science Videos
What is Lattice Energy?
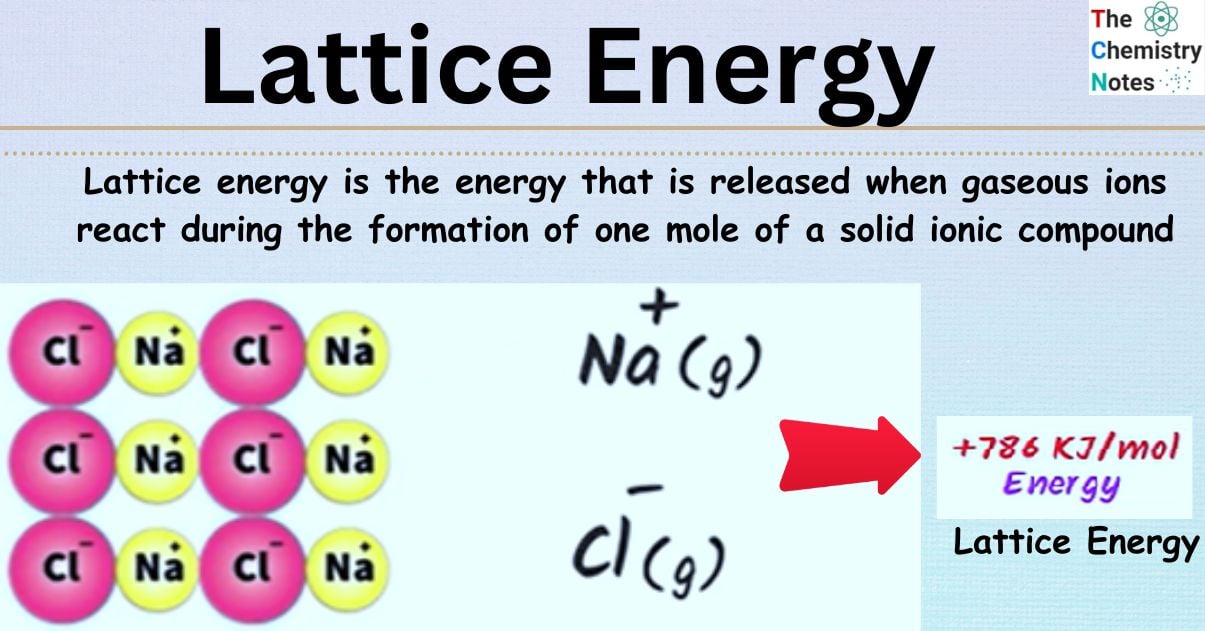
Lattice energy is the energy that is released when gaseous ions react during the formation of one mole of a solid ionic compound; however, it is also the energy that describes the energy that facilitates the dissociation of one mole of a solid ionic compound into its constituent gaseous ions.
Lattice energy can be described as a certain quantity of energy released when gaseous ions react when one mole of a solid ionic compound is formed. Whether the molecule forms or disassociate, either lattice energy can be lost (referred to as exothermic) or gained (referred to as endothermic). It is a method for determining the strengths of the forces that hold the atoms in a crystal lattice together. The fact that it may provide information on a variety of qualities, including hardness, volatility, and solubility, is one reason why lattice energy is so important.
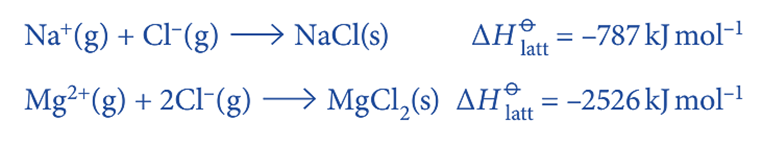
Note that:
- the ions that are gaseous are the ones that combine to form the ionic solid;
- the lattice energy is always exothermic; the value of (ΔHꝋlatt) is always negative; this is because the definition specifies the bonding together of ions, not the separation of ions; and the ionic solid always has a negative value for the lattice energy.
Due to the high exothermic value of the lattice energy, it may be deduced that the ionic lattice is particularly stable in relation to its gaseous ions. The lattice energy has a direct correlation to the strength of the ionic bonding that occurs inside the lattice.
It is not feasible to ascertain a compound’s lattice energy by using solitary direct experiment. Yet, we are able to compute a value for (ΔHꝋlatt) by utilizing a number of experimental values in conjunction with a type of energy cycle known as a Born–Haber cycle. In order to accomplish this, we will initially need to introduce two more forms of enthalpy change.
The term “lattice energy” is technically incorrect; what we’ve described is the “lattice enthalpy.” Nonetheless, lattice enthalpy is sometimes referred to simply as “energy” or “energy lattice.” When 1 mole of an ionic compound is created from its gaseous ions at 0K, the resulting shift in internal energy is referred to as the lattice energy of the complex. The values of lattice enthalpy and energy are quite close to one another.
Factors Affecting Lattice Energy
The lattice energy of an ionic compound is determined mostly by the size of the charges on the ions and the distance between them.
Ionic Radius:
Lattice energy decreases with increasing ionic radius. To clarify, the force of attraction between two opposing ions is greatest when the ions themselves are small. The lattice energy goes down as the distance grows larger. Ionic compounds with lower lattice energies are composed mostly of bigger ions because of the greater space between them. Ionic compounds with smaller ions have higher lattice energies because of the smaller ions.
Example: In comparison to that of potassium fluoride (KF), the lattice energy of cesium fluoride (CsF) is more endothermic (KF). As fluoride (F–) ions are present in both compounds, the lattice energy difference must result from the presence of the different cations, cesium (Cs+) in CsF and potassium (K+) in KF.
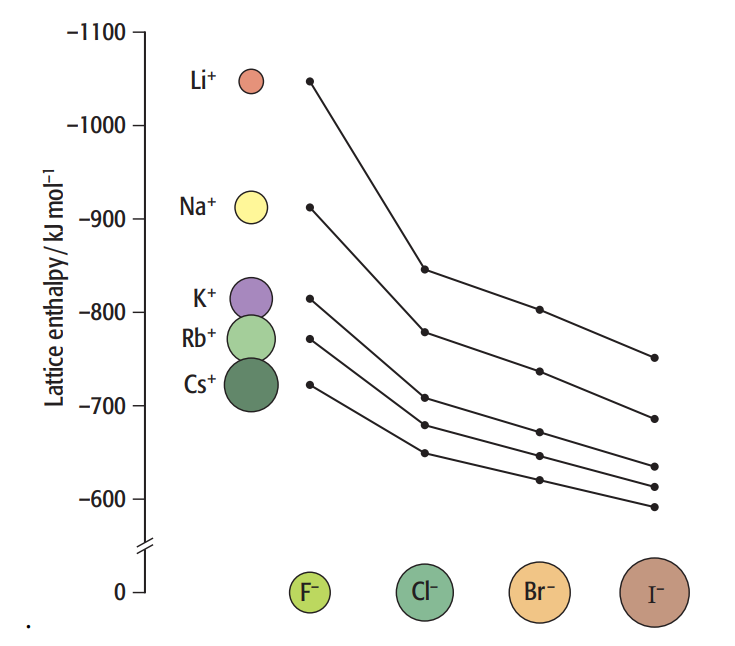
The ionic bond energy between alkali metals and halogens is tabulated below (in kJ/mol).
| F– | Cl– | Br– | I– | |
| Li+ | 1036 | 853 | 807 | 757 |
| Na+ | 923 | 787 | 747 | 704 |
| K+ | 821 | 715 | 682 | 649 |
| Rb+ | 785 | 689 | 660 | 630 |
| Cs+ | 740 | 659 | 631 | 604 |
[Image Source: Savemyexams]
Potassium belongs to Period 4 and Group 1 and Cesium belongs to Period 6 and Group 1. In other words, the Cs+ ion is bigger than the K+ ion. Cs+ and F– ion electrostatic forces are less than those of K+ and F– ions. Thus, CsF has a smaller exothermic lattice energy than KF.
Ionic Charge:
The lattice energy grows in proportion to the atomic charge. Hence, a larger charge on the ions results in a stronger ionic connection. Each ion in an ionic lattice is attracted to every other ion due to electrostatic forces. The electrostatic force of attraction between ions is strong if and only if the total charge of the ions is large; hence, a more positively charged lattice will be more stable.
Example: Calcium chloride and potassium chloride have very similar crystal structures, however calcium chloride has a higher lattice energy. Because calcium cations have a more powerful positive charge (+2) than potassium cations do (+1)
Polarizability of the Ions:
Lattice energy generally decreases with the polarizability of the ions. This is due to the fact that the forces binding polarizable ions together are weaker since they may more readily deform their electron clouds in response to the electrostatic forces of the other ions.
Ionization Energy:
The ionization energy of the ions is often correlated with the lattice energy. This is so that the ion will be more stable and have a higher lattice energy as a greater ionization energy indicates that it takes more energy to remove an electron from an atom.
Electron Affinity:
Lattice energy often rises in direct proportion to the ions’ electron affinities. This is because an atom requires more energy to accept an electron, hence an ion with a greater electron affinity will be more stable and have a higher lattice energy.
Lattice Energy Trends in Periodic Table
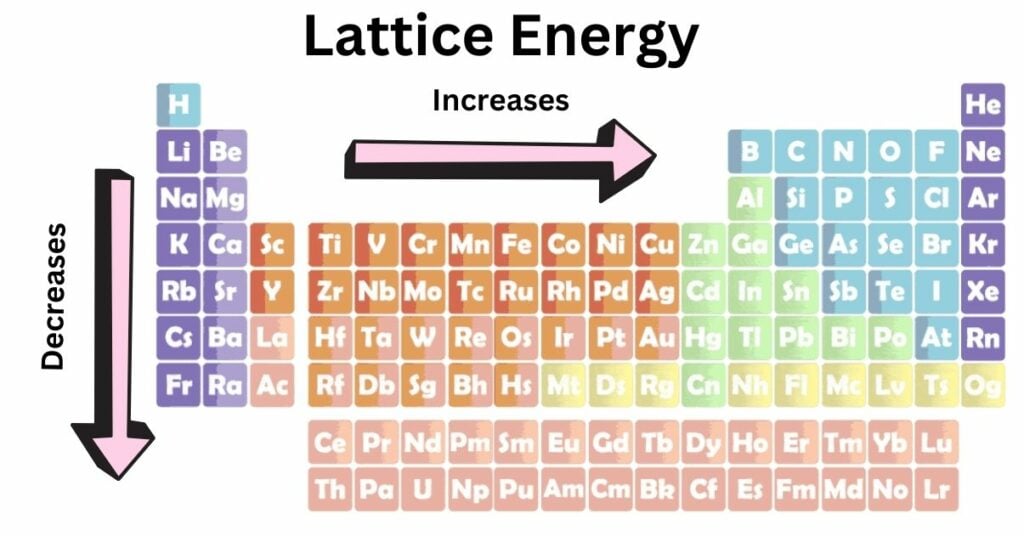
- The charge on the ions is the primary factor impacting lattice energy; the greater the ionic charge, the greater the lattice energy. This is due to the fact that ions with larger charges have a stronger attraction toward one another. As a consequence of this, a greater amount of energy is released when bonds are established between them.
- Smaller ions (small ionic radii) often have higher lattice energy, according to general trends in ionic radius because the greater the attraction between ions is as their separation grows smaller.
The atomic charge rises over a period, while the ionic radius rises over a group. Because of this, the lattice energy rises from left to right throughout a period and falls from top to bottom inside a group.
Comparison of Lattice Energy and Lattice Enthalpy
The following equation may be used to represent the molar lattice energy of an ionic crystal in terms of molar lattice enthalpy, pressure, and volume change:
ΔLatticeU = ΔLatticeH – pΔVm
Where:
- ΔLatticeU denotes the molar lattice energy.
- ΔLatticeH denotes the molar lattice enthalpy.
- ΔVm is the change in volume (per mole).
- p is the pressure.
Hence, while computing the lattice energies of ionic solids, the external pressure is also taken into account.
Calculation of Lattice Energy
Lattice energy turns out to be empirically indeterminate. Yet, we may utilize the Born-Haber Cycle to determine the thermodynamic lattice energy of ionic solids.
The Born-Haber cycle is a method used to determine the enthalpy of formation or lattice energy of ionic compounds made from gaseous ions.
The solid ionic compound is assumed to be the end result in the Born-Haber cycle. The cycle therefore always begins with the components in their default condition. The elements are changed into solid lattice, gaseous ions, and finally, gaseous ions.
An ionic compound’s lattice energy is the amount of energy necessary to break it down into its gaseous ions. The Born-Haber cycle includes the following steps:
- calculating the compound’s enthalpy of production from its constituent parts. Calorimetry or other techniques can be used to accomplish this.
- determining the negative ion’s electron affinity. This is the power necessary to create a negative ion by adding an electron to a neutral atom.
- calculating the positive ions ionization energy. This is the power needed to take an electron out of a neutral atom so that it can become a positive ion.
- calculating the positive ion’s sublimation enthalpy. The positive ion must be vaporized using this energy.
- calculating the negative ion’s vaporization enthalpy. The negative ion must be vaporized using this energy.
Lattice energy = Enthalpy of Formation + Electron Affinity + Ionization Energy – Enthalpy of Sublimation of Positive Ion – Enthalpy of Vaporization of Negative ion
Lattice Energy of NaCl
Normal NaCl formation is described by the following reaction.
Na (s) + 12Cl2 (g) → NaCl (s)
Step 1: Convert the reactants into ionic gas components.
- Na (s) → Na (g)
Na (g) → Na+(g) + e− - 12Cl2 (g) → Cl (g)
Cl (g) + e− → Cl− (g) - Na+ (g) + Cl− (g) → NaCl (s)
The “lattice” compound is created at this final stage of processing.
Step 2: Divide the reaction into its component parts and analyze each separately in line with Hess’s law.
NaCl (s) → Na (s) + 12Cl2 −ΔHf,NaCl(s) = +411 kJ; Na, Δ=107 kJ
Na (g) → Na+ (g) + e− IE1,Na (g) = 502 kJ
12Cl2 (g)→Cl(g) 12 ΔHbond,Cl2 (g) = 12×242 kJ
Cl (g) + e−→ Cl− (g) EA1, Cl (g) =−355 kJ
Na+(g) + Cl− (g) → NaCl (s)
Step 3: The final Born-Haber Cycle equation is formed by combining these elements
ΔHcycle=ΔHf,NaCl(s) + ΔHsub,Na + IE1,Na(g) + 12ΔHbond,Cl2(g) − EA1,Cl(g −ΔHlattice
Step 4: Solve for lattice variable: ΔHlattice,NaCl(s)
=−[411+107+502+12(242)−355]kJ
Lattice energy of NaCl=−786 kJ
Lattice Energy (U)
The amount of energy needed to fully separate one mole of an ionic solid into its gaseous ions is known as lattice energy (U).
One can find the Lattice Energy formula in:
U = – (Z×e)² / (4πεor)
where
Z = Charge of the Ion
e = Electronic Charge
εo = Vacuum Permittivity
r = Distance between the Ionic Centres
Examples of Lattice Energy
Sodium Chloride (NaCl)
Sodium chloride (NaCl) crystal develops when sodium ion (Na+) and chloride ion (Cl–) combine, releasing 787.3 kJ of energy in the process.
Na+ (g) + Cl– (g) → NaCl (s) (ΔHꝋlatt= –787.3 kJ/mol)
Calcium oxide (CaO)
CaO crystal develops when the calcium ion (Ca2+) and oxide ion (O2-) combine, releasing 3414 kJ of energy in the process.
Ca2+ (g) + O2- (g) → CaO (s) (ΔHꝋlatt = -3414 kJ/mol)
References
- Theodore Lawrence Brown, Eugene, H., Bursten, B. E., Murphy, C. J., Woodward, P. M., Stoltzfus, M. W., & Lufaso, M. W. (2018). Chemistry : the central science (14th ed.). Pearson.
- House, J. E., & Kathleen Ann House. (2016). Descriptive inorganic chemistry. Amsterdam ; Boston ; Heidelberg ; London ; New York ; Oxford ; Paris ; San Diego ; Singapore ; Sydney ; Tokyo Elsevier.
- https://www.geeksforgeeks.org/lattice-energy/
- https://byjus.com/chemistry/lattice-energy/#:~:text=The%20two%20primary%20factors%20that,the%20distance%20between%20the%20ions.
- https://chemistrytalk.org/what-is-lattice-energy/
- https://www.savemyexams.co.uk/a-level/chemistry/cie/19/revision-notes/5-physical-chemistry-a-level-only/5-1-chemical-energetics-a-level-only/5-1-2-factors-affecting-lattice-energy/
- https://www.chemistrylearner.com/lattice-energy.html

God bless you sister great effort