The cornerstone of quantum mechanics is the Schrödinger equation. If electrons, atoms, and molecules exhibit wave-like characteristics, then a mathematical function must exist that is the solution to a differential equation that characterizes electrons, atoms, and molecules. The solution of this differential equation, is also known as the wave function. The equation is named after Erwin Schrödinger, who received the Nobel Prize in physics in 1933 alongside Paul Dirac.

Interesting Science Videos
What is Schrödinger Equation?
The Schrödinger equation, also known as Schrödinger’s wave equation, is a partial differential equation that employs the wave function to explain the dynamics of quantum mechanical systems. This equation can be used to determine the trajectory, positioning, and energy of these systems.
The Schrödinger wave equation is a mathematical expression that accounts for the electron’s nature as a matter wave inside an atom when describing the energy and position of the electron in space and time.
It is based on three factors. They are;
- Classical plane wave equation,
- Broglie’s Hypothesis of matter-wave, and
- Conservation of Energy.
Derivation of the Schrödinger Wave Equation
Classical Plane Wave Equation
A wave is a disturbance of a physical quantity that oscillates or moves harmonically around its axis. The disturbance is transmitted sinusoidally to its neighbors.
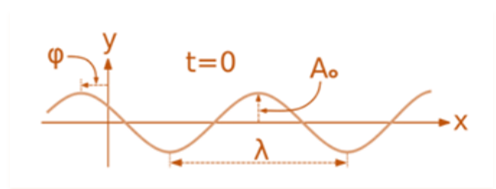
A second-order partial differential equation of a scalar variable in terms of one or more space variables and time variables constitutes the equation for the wave. The equation for a single-dimensional wave is:
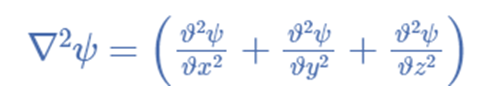
For illustration, the formula for a plane progressive sinusoidal wave’s amplitude (y) is:
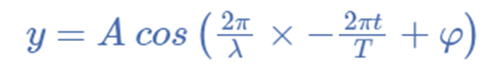
where;
t is the time in seconds,
A is the maximum amplitude,
T is the period and
φ is the phase difference of the wave.
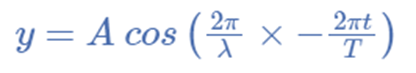
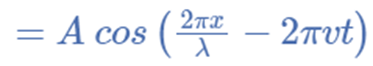
The identical equation can typically also be written as,
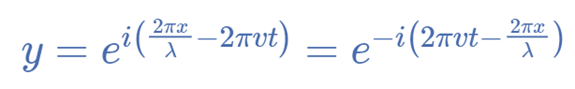
The Time-Dependent Schrödinger Equation
The time-dependent Schrödinger equation describes how a particle’s wave function changes over time and space. Free particles make for an easy case to think about because their solution is a plane wave and their potential energy V = 0.
The time-dependent Schrödinger wave equation form depends on the physical context of the system being described because it describes an evolving system over time. Schrödinger wave equation time-dependent form is:
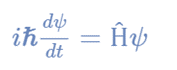
where,
Ψ is the state vector of the quantum system
t is time
Ĥ is an observable, Hamiltonian operator.
A system’s total energy, including kinetic and potential energy, is represented by an operator known as the Hamiltonian. The set of all outcomes that can be obtained when the total energy of the system is measured is known as its spectrum, also known as the system’s energy spectrum or its set of energy eigenvalues.
Some of Schrödinger equation’s for its time-dependent form
The Schrödinger wave equation’s derivation for its time-dependent form is provided below.
Maxwell’s equation is thus
∇2Ψ (x, y, z, t) − (1/ c2) (∂2Ψ (x, y, z, t)/ ∂t2) = 0
The Laplacian operator
∇2 = (∂2/ ∂x2) + (∂2/ ∂y2) + (∂2/ ∂z2)
The form of a wave as a function is
Ψ(x) = f (2πx/ λ)
Euler’s formula
e±iθ = cos θ ± i sin θ
The analogous structure of the time-dependence of the wave
T(t) = f (2πνt)
A wave function of the form
Ψ (x, t) = exp [2πi ((x/ λ) − νt)]
Using the Planck formula (E = hν) and de Broglie formulas (p=h/ λ)
Ψ (x, t) = exp [i (px−Et)/ ℏ]
Where
ℏ ≡ h/ 2π
The time derivative version becomes
∂Ψ/ ∂t = − (iE/ ℏ) exp[i(px−Et)/ ℏ]
iℏ (∂Ψ/ ∂t) = EΨ
−iℏ (∂Ψ/ ∂x) = pΨ
−ℏ2 (∂2Ψ/ ∂x2) = p2Ψ
The energy and momentum for a non-relativistic free particle
E = mv2/ 2 = p2/ 2m
iℏ (∂Ψ/ ∂t) = −(ℏ2/ 2m) (∂2Ψ/ ∂x2)
The energy and momentum for a nonrelativistic free particle
E = (p2/ 2m) + V(x)
The time dependent Schrödinger equation in 1D
iℏ (∂Ψ (x, t)/ ∂t) = [−(ℏ2/ 2m) (∂2/ ∂x2) + V(x)] Ψ (x, t)
The time dependent Schrödinger equation in 3D
iℏ (∂/ ∂t) Ψ (r⃗, t) = [−(ℏ2/ 2m) ∇2 + V (r⃗)] Ψ (r⃗,t)
Time-Independent Schrödinger Wave Equation
Schrödinger wave equation in its time-independent form describes the properties of stationary states, which are wave functions that have formed standing waves. The following is the expression for Schrödinger wave equation’s time-independent form.
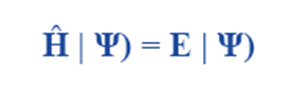
where
E is the energy of the system
Ĥ is an observable, the Hamiltonian operator
Schrödinger wave equation can only be expressed in its time-independent form if the Hamiltonian is not explicitly time-dependent. Even so, time is still a factor in the overall wave function. The Schrödinger wave equation derivation for the time-independent form is provided below.
The time-dependent Schrödinger equation in 3D is
iℏ (∂/ ∂t) Ψ (r⃗, t) = [−(ℏ2/ 2m) ∇2 + V (r⃗)] Ψ (r⃗, t)
For conservative systems, the energy is a constant, and the time-dependent factor form can be separated from the space-only factor
Ψ (r⃗, t) = ѷ (r⃗)e−iEt/ℏ
The time independent Schrodinger equation is
[− (ℏ2/ 2m) ∇2 + V(r⃗)] ѷ(r⃗) = E ѷ (r⃗)
Hamiltonian operator
The operator in mathematics is a rule that transforms observed properties into another property. A is an operator, for instance, if it can transform the property f(x) into another f(y). f(x)= f(y) The Hamiltonian operator is the sum of particle potential and kinetic energies calculated over three coordinates and time.
Hamiltonian operator = Ȟ = T + V = Kinetic energy + Potential energy
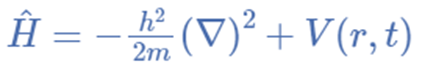
Physical Significance of Schrödinger wave Function
- The Bohr concept of an atom is straightforward. However, it is unable to account for the existence of multiple orbitals and the fine spectrum that results from them. It only applies to systems with one electron.
- There are numerous distinct solutions for the Schrodinger wave function that represent its characteristic amplitude, energy, and radius. The wave function’s calculation of the electron’s probability density reveals a variety of orbitals, each with its own energy and spatial distribution.
- Schrödinger equation may be used to explain the existence of multiple orbitals and the fine spectrum produced by all atoms, not just those that resemble hydrogen.
Schrödinger wave equation Applications
- It serves as the basis for wave mechanics.
- It supports the investigation of atomic structure.
- All of matter’s wave-like properties are reflected in it.
- It serves as the basis for wave mechanics.
References
- https://www.aakash.ac.in/important-concepts/physics/schrodingers-wave-equation
- https://byjus.com/jee/schrodinger-wave-equation/
- https://study.com/academy/lesson/schrodinger-wave-equation-overview-time-dependent-independent-equation.html
- https://unacademy.com/content/jee/study-material/chemistry/wave-function/
- Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 978-0-13-111892-8.
- Griffiths, David J. (2008). Introduction to Elementary Particles. Wiley-VCH. pp. 162–. ISBN978-3-527-40601-2

Thank you so very much it is really helpful