In cases where a reaction mechanism comprises multiple steps with comparable rates, identifying the rate-determining step can be challenging. Nonetheless, an intermediate compound is present in certain stages of the process. An intermediate refers to a chemical species that is not classified as either a reactant or a product in a given chemical reaction.

The steady-state approximation is a widely employed technique in chemical kinetics to obtain a rate law. The methodology relies on the presumption that an intermediate species involved in the reaction mechanism is depleted at the same rate as it is produced. The concentration of the substance remains constant throughout the duration of the reaction.
Interesting Science Videos
Approximations for Complex Reactions
Once a reaction has been identified as complex, the next step is to analyze the kinetic data and propose a mechanism for the reaction.
When studying the progress and mechanism of a chemical reaction, we encounter various concepts such as reaction coordinate and activated complex. The definition of a reaction coordinate is a function that takes into account all the coordinates of the species involved in a reaction within the space. The progress of a reaction can be measured by tracking its movement along the path of minimum potential energy, starting from the reactant molecules and ending with the product molecules. The activated complex is located at the point where the reaction coordinate has the maximum potential energy.
Currently, the atoms of the reactants possess a configuration of maximum energy due to mutual repulsion. Two approximations are commonly employed to explain the mechanism of a complex reaction. These are.
- Equilibrium approximation
- Steady-state approximation
What is Steady-State Approximation?
The Steady-State Approximation, also known as the quasi-steady-state approximation, involves assuming that the concentrations of all reactive intermediates experience negligible rates of change. This approximation is typically reliable when the concentrations of the intermediates are low, as variables with small time derivatives tend to have small values if they do not oscillate rapidly.
The Steady State Approximation is a method used in chemical kinetics to simplify the analysis of reaction mechanisms. It assumes that the concentration of certain reactive intermediates remains constant over time, allowing for the derivation of simplified rate equations. This approximation is particularly useful in cases where the rate of formation and consumption of intermediates is much faster than the rate of the overall reaction.
The study of chemical kinetics, which pertains to the rate of a chemical reaction and its corresponding rate law, is a crucial aspect of physical chemistry. Understanding the free energy changes associated with a particular process provides insight into the likelihood of its occurrence.
In order to determine the rate of a chemical reaction, the fields of chemical kinetics and rate law are essential. The steady-state approximation technique is a commonly employed method for determining the precise rate of a chemical reaction.
When studying reactants under conditions where the slowest rate-determining step is not present, the steady-state approximation is used for the transient intermediate species.
Reactants: I1 → I2 → I3……..In
The reactants follow a sequential process where I1 transforms into I2, which then transforms into I3, and so on until the final product In is obtained.
The rate of intermediate formation is equivalent to its rate of decomposition.
d [I1]/ d t = d [I2]/d t = 0
The steady-state approximation is a technique utilized to verify the consistency of the rate law. When the value of the derivative is equal to zero, the system is said to be in a steady state.
Steady state of reaction
Reaction: aA + bB → gG + hH
The above reaction is in the steady state if the rates of loss of all reactants and the rates of production of all products which appear in the balanced reaction equation are equal:
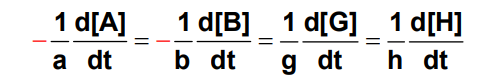
In the other words it means that intermediates are present at very low concentrations and the rates of their productions and loss are equal.
Steady-State Approximation for Unimolecular Kinetics
The Steady State Approximation is a useful tool for analyzing unimolecular kinetics.
According to the steady state approximation, the concentration of molecule B, which is the intermediate compound, remains consistently low or even negligible at all times without any significant changes.
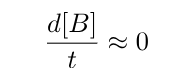
The rate of change of concentration of B with respect to time is approximately zero.
For this approximation to be valid, the consecutive reaction system must satisfy two commonly observed criteria:
- The concentration of B is generally much lower compared to that of A or C.
- The rate at which A reacts to form B is significantly slower than the rate at which B reacts to form C. This implies that the rate determining step is the formation of B by A.
Several consecutive reaction systems fulfill these criteria. B is frequently observed to behave as an unstable intermediate, resulting in an initial increase in concentration until it reaches a specific low threshold. Any excess B that is produced quickly converts to C due to its instability, which happens much faster than the production of B. Mathematically speaking, it can be inferred that kb denotes a significantly greater quantity than ka.
Application of Steady-state Assumption
To apply the Steady State Assumption, we assume that a system is in a state of equilibrium where the input and output rates are equal and the system’s behavior is constant over time.
When both criteria are fulfilled, the steady state approximation significantly simplifies the mathematical calculations. Specifically, it provides us with a means to establish a direct relationship between the concentrations of A and B.
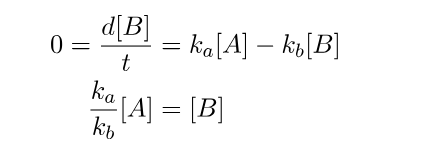
This enables us to derive an expression for the concentration of C as a function of time more efficiently.
Next, we will apply the first-order rate law that relates the change in A to express C as a function of time.
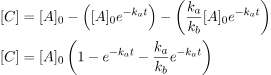
If ka is much smaller than kb (ka/kb ≈ 0), we can often simplify the equation. By neglecting the third term in the parenthesis, we can obtain:
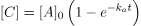
Solved Example oF Steady-state Approximation
Derive the rate law for this reaction using steady-state approximation.
2N2O5 → 4NO2 + O2

NO and NO3 are intermediates.
production rate of NO = k2[NO3][NO2]
consumption rate of NO = k3[NO3][NO]
A steady-state approach makes use of the assumption that the rate of production of an intermediate is equal to the rate of its consumption. Thus, we have
k2 [NO3][NO2] = k3[NO3][NO]
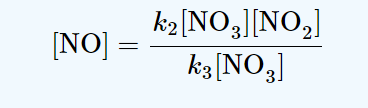
production rate of NO3 = kf [N2O5]
consumption rate of NO3 = k2[NO3][NO2] + k3[NO3][NO] + kb[NO3][NO2]
Now, using Steady-state approximation;
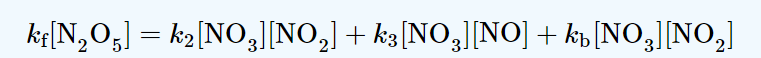
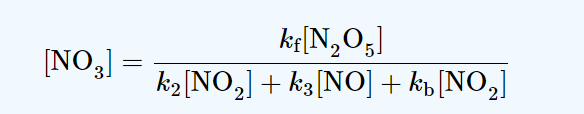
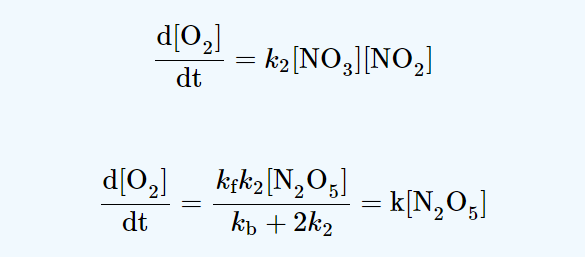
Enzymes and the Steady-State Approximation
The concept of approximation holds significant importance in enzyme kinetics as it helps in formulating the equation for the reaction velocity.
The steady-state approximation is applicable to catalytic reactions, such as the enzyme example, because intermediates are not present in the net equations.
Enzyme mechanisms use a certain kind of multistep reaction. In living things, an enzyme functions as a catalyst.
The creation of a product, P, and the unmodified enzyme is caused by the binding of a reactant called a substrate to the enzyme to form an enzyme-substrate complex (ES). This procedure appears as follows:
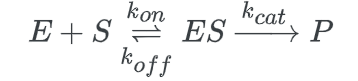
The Michaelis-Menten equation is used to determine the rate of reaction, often known as the velocity of reaction. The equation is:
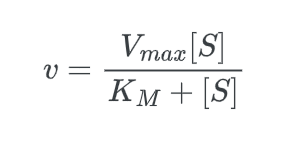
Where
- Vmax is the maximum reaction velocity.
- [S] is the concentration of the substrate.
- KM is the Michaelis constant. The Michaelis constant is the “rate constant” for enzymes.
We can derive this formula using the steady-state approximation.
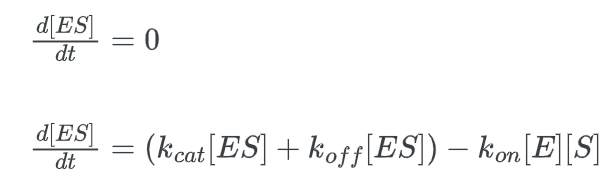
We must translate [E] to [ET] in order to end up at our final equation. [E] represents the concentration of the “free” enzyme, or more precisely, the concentration of enzyme that is unattached to a substrate. But since [ET] represents the total enzyme concentration, it also takes into account the bound enzymes.
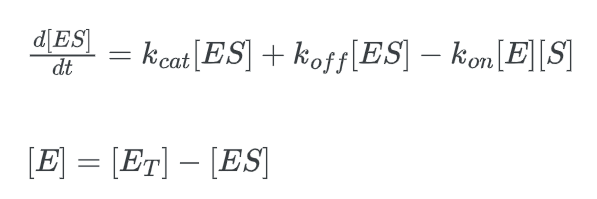
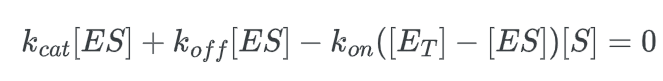
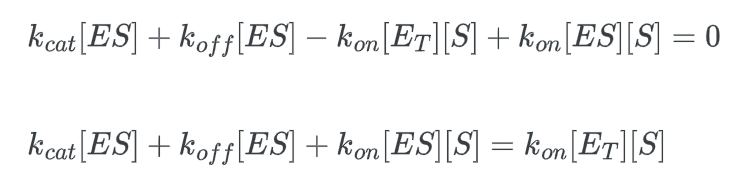
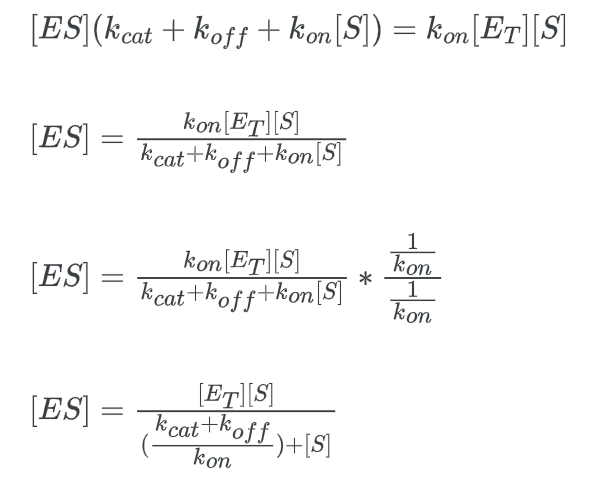
multiply this expression by kcat:
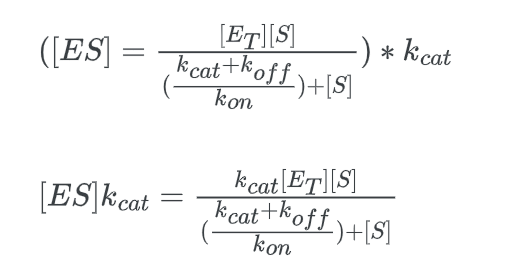
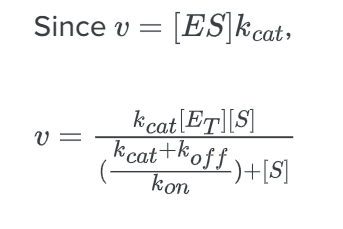
Now comparing the above equation with the following equation.
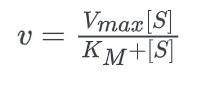
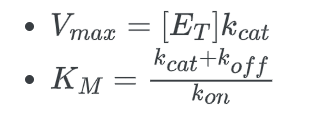
References
- https://www.studysmarter.co.uk/explanations/chemistry/kinetics/steady-state-approximation/
- https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Kinetics/04%3A_Reaction_Mechanisms/4.12%3A_Steady-State_ Approximation
- https://chemistrytalk.org/steady-state-approximation/
- https://byjus.com/chemistry/steady-state/
- https://pressbooks.bccampus.ca/chbe220/chapter/steady-state-approximation/
- https://chemistrytalk.org/steady-state-approximation/
- https://www.studysmarter.co.uk/explanations/chemistry/kinetics /steady-state-approximation-example/
