The Nernst equation is very useful in analytical chemistry as well as in significant life processes like nerve conduction and membrane potential. Electrochemical cells and the Nernst equation calculates the pH of solutions, solubility products, constant equilibrium, and other thermodynamic properties, as well as potentiometric titrations and the calculation of cell membrane resting potentials.
The relationship between the potential of the electrode and the potential of the reference electrode is thus provided by this equation. Additionally, it also helps to compute the Gibbs free energy and forecast the spontaneity of an electrochemical reaction.

Interesting Science Videos
What is Nernst Equation?
A chemical thermodynamic relationship known as the Nernst equation is applicable in electrochemistry to determine a reaction’s reduction potential (half-cell or full-cell reaction) from the standard electrode potential, absolute temperature, the number of electrons involved in the oxydo-reduction reaction, and activities (often approximated by concentrations) of the chemical species undergoing reduction and oxidation, respectively.
The Nernst equation establishes a relationship between an electrochemical cell’s cell potential, the standard cell potential, temperature, and the reaction quotient. Moreover, this equation can be used to calculate the cell potentials of electrochemical cells even in unusual circumstances.
Walther Nernst, a German physical chemist who created the equation, was honored with its naming.
Expression for Nernst equation
The Nernst equation calculates the potential of an electrochemical cell at any known temperature, pressure, and concentration. The equation compares the cell’s reduction potential under standard conditions to that under non-standard conditions (298K, 1 atm, and 1 M concentration).
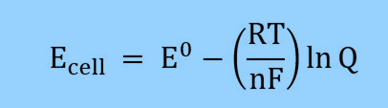
where
- ECell = cell potential
- E0 = Cell potential under standard conditions
- R = Universal gas constant (8.314 J/(mol*K))
- T = Temperature
- n = Number of electrons transferred in the reaction
- F = Faraday constant (96485 C/mol)
- Q = Reaction Quotient
The equilibrium constant (K) and Q are identical, but Q is not always present at equilibrium. Since we are looking for non-standard cell potentials, using Q makes sense.
This equation helps to determine the potential of half-cell reactions or cell potentials for different electrochemical cells.
There are various other ways to write the equation that reduce the term RT/nF to a constant. One way to make the equation more like the pH equation is, for example, to change the natural log to log.
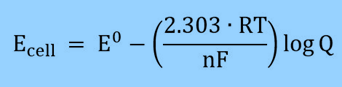
It is possible to simplify the equation for cells at 25 °C
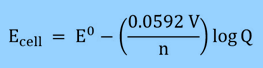
Nernst Equation for Electrode Potential
With temperature and species concentration, electrode potential varies drastically. The standard set of conditions has therefore been established in order to define a specific reference for electrode potentials. The potential is referred to as “Standard Potential” if it is measured in these circumstances.
It allows for the precise determination of equilibrium constants and connects the measured cell potential to the reaction quotient (including solubility constants). The expression of Nernst equation is:
E cell=E°cell−0.0591/n log Q at 25 °C
The aforementioned equation shows that the reaction quotient Q of the reaction affects the electrical potential of an electrode.
Therefore, if we want to calculate the reduction potential of the Cu electrode, we must take into;
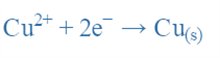
In the Nernst Equation, we get:
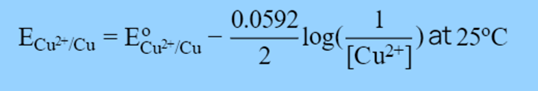
This way we can determine the ECu2+/Cu for the Copper electrode at any temperature and concentration if we know the standard reduction potential of the Copper electrode i.e., E°Cu2+/Cu.
Nernst Equation for EMF of a cell
The Nernst Equation can also calculate the cell potential under non-standard conditions. It allows for the precise determination of equilibrium constants and connects the measured cell potential to the reaction quotient (including solubility constants).
The Nernst equation is as follows:
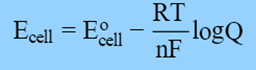
i.e. E cell = E°cell − 0.0591/n log Q at 25 °C
According to the equation above, a reaction’s reaction quotient Q determines a cell’s electrical potential.
Using a cell: Zn∣Zn2+∣∣ H+∣H2∣Pt
For the Chemical reaction:
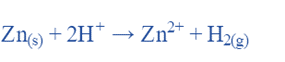
The Nernst equation can also determine the cell potential if the ion concentrations and H2 pressure are not 1.0 M and 1.0 atm, respectively:
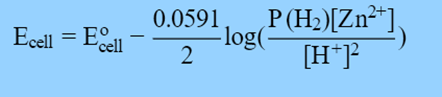
Derivation
Consider a metal that has come into contact with its own salty water. Both possible and in equilibrium reactions of a metal losing an electron to become an ion and an ion gaining an electron to return to the atomic state are possible.
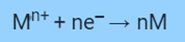
In a reduction reaction, an ion absorbs ‘n’ moles of an electron in opposition to an Ered reduction potential.
- The work done in the movement of electrons
Wred = nFEred
Where, one mole of electrons carries 96487 coulombs of electrical charge, or F, which stands for Faraday.
- Change in the Gibbs free energy is a sign of spontaneity and equals the most productive work that can be done in a process (aside from volume expansion).
Combining the Gibbs free energy change and work done:
Wred = nFEred = – ∆G or ∆G = – nFEred
- At standard conditions of 298K and one molar/one atmospheric pressure, the free energy changes by ∆G°. It is clear from the relationship mentioned above that
∆G° = – nFE°red
Where E°red is the reduction potential at standard conditions.
- As the reaction progresses, concentration is constantly changing, and the potential will drop along with it.
The concentrations must remain constant in order to produce the greatest amount of work or change in free energy. Only by conducting the reaction under a reversible equilibrium condition is this feasible.
A Vant Hoff isotherm for a reversible equilibrium reaction states:
∆G = ∆G° + RT ln K
Where,
- K is the equilibrium constant
- K = Product/Reactant = [M]n/[M]n+
- R is the Gas constant =8 .314J/K mole
- T is the temperature on Kelvin scale.
Substituting for free energy changes in Vant Hoff equation,
– nFEred = – nFE°red + RT ln [M]/[Mn+] = – nFE°red + 2.303 RT log [M]n/[Mn+]
Dividing both sides by – nF,
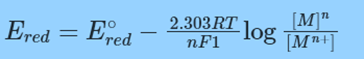
or
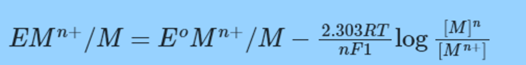
Metal activity is always regarded as being equal to one.
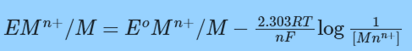
This describes the relationship between the reduction potential, which measures under non-standard conditions, and the standard electrode potential.
Nernst Equation for reaction at 298 K but different concentrations is;
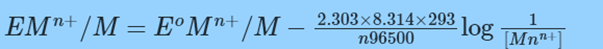

Application of Nernst Equations
Using the equation, one can determine:
- Under any circumstances, the single electrode reduction or oxidation potential
- Standard electrode potentials
- Comparing the relative ability as a reductive or oxidative agent.
- determining whether it is feasible to combine such single electrodes to create electric potential.
- Emf of an electrochemical cell
- unknown concentrations of ions
- The Nernst equation can also calculate the pH of solutions and the solubility of salts that are only marginally soluble.
- Used in the marine environment
- Helpful in figuring the potential of an ion with the charge “z” over the membrane.
Limitations of the Nernst Equation
It is possible to express an ion’s activity in terms of concentration because it is almost infinitely small in very dilute solutions. For solutions with very high concentrations, the ion concentration does not match the ion activity. The true activity of the ion must be determined experimentally to apply the Nernst equation in such circumstances.
This equation also has the drawback of not being accurate when an electrode current is flowing through it, which makes it impossible to measure cell potential. This is true because the current flow affects how the ions behave on the electrode surface. When a current flows through the electrode, additional factors like resistive loss and overpotential must also be taken into account.
Did You Know?
- In 1920, Nernst’s work on thermochemistry earned Walther Hermann Nernst (the chemistry Nobel Prize.
- The third law of thermodynamics is yet another well-known discovery made by Nernst.
- One of the main uses of the Nernst equation is thus to determine electrochemical cell potentials. The majority of battery types are powered by electrochemical cells! Other surfaces, such as plating gold onto jewelry, can be covered with thin layers of materials using these cells.
References
- Feiner, A.-S.; McEvoy, A. J. “The Nernst Equation.” J. Chem. Educ. 1994, 71, 493.
- https://byjus.com/jee/nernst-equation/
- https://chem.libretexts.org/Bookshelves/Analytical_Chemistry/Supplemental_Modules_(Analytical_Chemistry)/Electrochemistry/Nernst_Equation
- https://www.savemyexams.co.uk/a-level/chemistry/cie/22/revision-notes/5- physical-chemistry-a-level-only/5-4-electrochemistry-calculations–applications-a-level-only/5-4-5-nernst-equation/
- https://en.wikipedia.org/wiki/Nernst_equation#Significance_in_other_scientific_ fields
- https://unacademy.com/content/jee/study-material/chemistry/nernst-equation-and-its-applications/
- https://chemistrytalk.org/nernst-equation/
- Bard, Allen J.; Faulkner, Larry R. (2001). “Chapter 2. Potentials and Thermodynamics of Cells – See: 2.1.6 Formal Potentials”. Electrochemical methods: Fundamentals and applications (2 ed.). New York: John Wiley & Sons
