A solution is said to have abnormal colligative properties if its experimentally measured colligative property differs from that calculated theoretically using Van’t Hoff factor.
The colligative property is affected by the number of solute particles in the solution but not by their nature. Abnormal values occur when a dissolved solute experiences a molecular change in solution, such as dissociation or association. The observed (or abnormal) colligative property may be greater or less than the theoretical value.

Interesting Science Videos
Abnormal Colligative Properties due to Association and Dissociation
In most cases, the practical values of colligative properties roughly approach the theoretical values determined by their formula. However, in some circumstances, experimental values of colligative properties diverge significantly from theoretical values. These experimental values are known as anomalous colligative properties.
The dissociation and association of solute molecules have been used to explain the anomalous behavior of colligative characteristics.
Dissociation of solute molecules
Electrolytes, which dissociate in solvent (water), indicate a rise in the number of particles present in solution. As a result, the observed value of the colligative property exceeds the theoretical value.
Association of Solute Molecules
When a nonelectrolytes is dissolved in a nonpolar solvent such as benzene, it undergoes association, resulting in the formation of molecules with a greater molecular mass. As a result, the number of particles in the solution reduces. As a result, colligative properties such as osmotic pressure, boiling point elevation, and so on are lower than the theoretical value.
Van’t Hoff Factor (i)
The Van’t Hoff factor is defined as the ratio of particle concentration to substance concentration by mass when the substance is dissolved. It is represented by the letter ‘i’.
The Van’t Hoff factor describes the extent to which a substance associates or dissociates in a solution. The Van’t Hoff factor provides information on how solutes affect the colligative properties of solutions. This factor is named after the Dutch physical physicist Jacobus Henricus Van’t Hoff, who earned the first Nobel Prize in chemistry.
It is also defined as the ratio of the experimental value to the calculated value of the colligative property.
Van’t Hoff Factor, in terms of Molar Masses
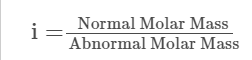
Van’t Hoff Factor, in terms of colligative properties.
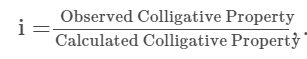
Van’t Hoff Factor in Terms of association and dissociation
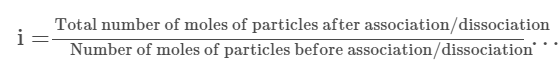
Values of Van’t Hoff Factor
| Dissociation | i<1 |
| Association | i>1 |
| No association or dissociation | i=1 |
Van’t Hoff Factor and Degree of Dissociation of Solute Molecules
Van’t Hoff factor is used to calculate the extent of dissociation of an ionic solute in terms of degree of dissociation (α).
The extent of dissociation or α is defined as the proportion of total ionic solute in a solution that dissociates into cations and anions.
Let us consider following reaction;
A ⇌ n B
1 mole of an electrolyte dissociates to give n number of ions, with a degree of dissociation of α.
At equilibrium:
After dissociation, the number of moles of undissociated solute remaining = 1−α
Moles of ions produced (after dissociation) = nα = α
Total number of particles moles (after dissociation) = 1–α+nα
Using the Van’t Hoff factor definition we get:
Van’t Hoff Factor (i) = (1–α+nα)/1
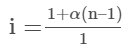
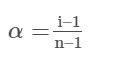
Knowing the value of Van’t Hoff factor (i) from observed molar mass and normal molar mass allows one to compute the value of α.
Van’t Hoff Factor and Degree of Association of Solute Molecules
The Van’t Hoff factor can be used to calculate the degree of association (α) and the extent of association of a non-polar solute.
The fraction of total non-polar solute present in the solution that undergoes association is defined as the degree of association.
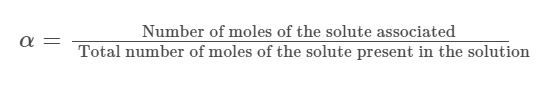
Let us consider a reaction where simple molecule A associates to form molecule An.
nA ⇌ An
Let the degree of association be α
At equilibrium:
Number of moles of unassociated solute left after association =1−α
Number of moles of associated molecules formed after association =α/n
Total number of moles of particles after association =1–α+α/n
From Van’t Hoff factor definition and using Eqn;
i=1–α+α/n
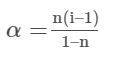
Knowing the observed molar mass, the normal molar mass and the number (n) of simple molecules that undergo association will allow you to compute the value of α.
References
- Tro, Nivaldo J. (2020). Chemistry : A Molecular Approach (Fifth ed.). Hoboken, NJ. pp. 613–614. ISBN 978-0-13-498889-4.
- https://gkscientist.com/vant-hoff-factor/
- https://unacademy.com/content/jee/study-material/chemistry/vant-hoff-factor-and-its-significance/
- Atkins, Peter W.; de Paula, Julio (2010). Physical Chemistry (9th ed.). Oxford University Press. ISBN 978-0-19-954337-3.
- Chisholm, Hugh, ed. (1911). “van’t Hoff, Jacobus Hendricus” . Encyclopædia Britannica (11th ed.). Cambridge University Press.
- https://www.embibe.com/exams/vant-hoff-factor/#Value-of-Van%E2%80%99t-Hoff-Factor
