The concept of absolute and relative error pertains to the degree of approximation error in a given data value. It represents the difference between the exact value and the approximated value. Absolute error is the number of discrepancies, while relative error is calculated by dividing the absolute error by the data value.

The concept of absolute error involves calculating the magnitude of the difference between the measured value and the true value. On the other hand, the relative error involves determining the absolute error in relation to the size of the measurement.
Interesting Science Videos
What is Absolute Error?
Absolute error is the numerical value that represents the difference between a measured value and the true or exact value.
The concept of absolute error pertains to the degree of deviation between a measurement and its actual value, or the level of imprecision associated with a measurement.
The formula for Absolute Error
- The formula for calculating the absolute error involves subtracting the measured value from the actual value.
Absolute Error = |True Value – Measured Value|
- The formula for computing the absolute error value is derived from the comparison between the actual value of a quantity, denoted as x, and its measured value, denoted as x0
Δx = x0 – x
The term “absolute error” is denoted by Δx.
When multiple measurements are taken into account, it is appropriate to determine the arithmetic mean of the absolute errors of each individual measurement as the ultimate absolute error.
Absolute Error Example:
A measurement is 24.87 mm and the true or known value is 27.00 mm. Find the absolute error.
Absolute Error = |27.00 mm – 24.87 mm|= 2.13 mm
Note absolute error retains its units of measurement.
Illustration of Absolute Error
When measuring the width of a book using a ruler with millimeter marks, the precision of the measurement is limited to the nearest millimeter. The book’s dimensions were measured and found to be 75 mm. The measurement is reported with an absolute error of 75 mm and a precision of +/- 1 mm. A discrepancy of 1 mm exists between the measured value and the true value, which is known as the absolute error. It should be noted that the absolute error is expressed in the same units as the measurement being taken.
In some cases, it may be the case that you possess a value that is either known or calculated, and you wish to utilize absolute error as a means of conveying the proximity of your measurement to the ideal value. The concept of absolute error involves calculating the numerical difference between the anticipated or predicted value and the actual value.
What is Relative Error?
The concept of relative error refers to the difference between an approximate or measured value and the true value of a quantity.
The utilization of relative error allows for a contextualized understanding of absolute error by evaluating the magnitude of the absolute error in relation to the magnitude of the actual value. It should be noted that the units cancel out during this computation, resulting in a dimensionless (or unitless) relative error.
The formula for Relative Error
- The formula for calculating relative error is given by taking the absolute value of the difference between the true value and the measured value, and then dividing this result by the true value.
Relative Error = |True Value – Measured Value| / True Value
Relative Error = Absolute Error / True Value
- The determination of the relative error of a measured quantity involves the use of the following formula, where x represents the true value of the quantity, x0 represents the measured value, and Δx represents the absolute error.
Relative error = (x0 – x) / x = (Δx) / x
Illustration of Relative Error
As an illustration, in a scenario where a driver’s speedometer indicates a velocity of 60 miles per hour (mph), the actual speed of the car is 62 mph. The calculation of the absolute error of the speedometer involves subtracting the measured value of 60 mph from the true value of 62 mph, resulting in an absolute error of 2 mph. The measurement’s relative error is calculated to be 0.033 or 3.3% by dividing 2 mph by 60 mph.
Absolute and Relative Error in Numerical Analysis
Numerical analysis is concerned with the approaches for identifying the approximations and the absolute mistakes in these calculations. In contrast to the relative error, which indicates the size of the error in relation to the correct value, the absolute error indicates the size of the error. In the context of numerical computation, errors may arise as a result of various factors.
- Round-off error refers to the discrepancy that arises when a numerical value is approximated by rounding it to a certain number of decimal places or significant figures.
- The truncation error is a numerical analysis concept that arises when an approximation method is used to solve a mathematical problem.
Absolute Accuracy Error
The concept of absolute accuracy error refers to the degree of deviation between a measured value and its true or expected value.
The term “Absolute Error” is alternatively referred to as “Absolute Accuracy Error.”
The formula can be expressed as follows:
E = x experimental – x true
Even though the formula has numerous names, it is still the same formula. The term “x experimental” refers to the measurement obtained through experimentation, while “ x true” denotes the actual or true measurement.
Mean Absolute Error (MAE)
The Mean Absolute Error (MAE) is the average of all absolute errors. The calculation of the mean absolute error involves the computation of the arithmetic mean of the absolute differences between the observed values and the corresponding predicted or estimated values in a given dataset. The mean absolute error is derived by dividing the summation of all absolute errors by the total number of errors.
The mathematical expression for Mean Absolute Error (MAE) is as follows:
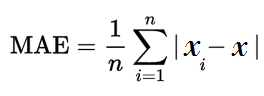
Where:
- n = the number of errors,
- Σ = summation symbol (which means “add them all up”),
- |xi – x| = the absolute errors.
Mean Absolute Error Example
The weight of an individual was measured thrice, yielding values of 126 lbs, 129 lbs, and 127 lbs. Based on the available data, it can be inferred that the individual’s actual weight is 127 pounds. What is the value of the mean absolute error for the given measurements?
Mean Absolute Error = [|126-127 lbs| + |129-127 lbs| + |127-127 lbs|] / 3 = 1 lb
Absolute Precision Error
The concept of absolute precision error pertains to the standard deviation of a given set of measurements, and is mathematically represented by the following formula:
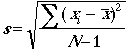
Where:
- Σ = the summation symbol.
- xi is the ith value (e.g. 1st, 2nd…),
- x̄ = the sample mean,
- N = the sample size.
Difference Between Absolute and Relative Error
| Absolute Error | Relative Error |
| The absolute error serves as a measure of the degree of uncertainty associated with a given measurement. In other terms, it determines how much the true value can differ from the experimental value. | The concept of relative error pertains to the difference that exists between an estimated or measured value and the true value of a given quantity. |
| Absolute error is the magnitude of the difference between the exact value and the approximation. | The relative error is calculated by dividing the absolute error by the magnitude of the exact value. |
| Absolute error is a Δx value (+ or – value), where x is variable; it is the physical error in a measurement. It is also known as the actual error in a measurement. | The relative error is the ratio of absolute error (Δx) to the measured value (x). It is expressed either as a percentage (percentage error) or as a fraction (fractional uncertainty). |
| It has the same units as the measured value. For example, if you measure the length of a book in centimeters (cm), the absolute error also has the same units. | The relative error can be expressed as a fraction or as a percentage. However, both do not have a unit in the value. |
| Absolute Error = |True Value – Measured Value| | Relative Error = |True Value – Measured Value| / True Value |
Video on Absolute and Relative Error
References
- Helmenstine, Anne Marie, Ph.D. “Absolute and Relative Error Calculation.” ThoughtCo, Aug. 26, 2020, thoughtco.com/absolute-and-relative-error-calculation-609602.
- Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press - Helfrick, Albert D. (2005). Modern Electronic Instrumentation and Measurement Techniques. ISBN 81-297-0731-4.
- https://sciencenotes.org/absolute-and-relative-error-and-how-to-calculate-them/
- Steel, Robert G. D.; Torrie, James H. (1960). Principles and Procedures of Statistics, With Special Reference to Biological Sciences. McGraw-Hill.
- Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.
- https://byjus.com/maths/absolute-and-relative-error/
- https://unacademy.com/content/jee/study-material/mathematics/absolute-and-relative-error/

