The term ‘atomic orbital’ refers to the physical space or region around an atom’s nucleus where the probability of a specific electron being present is greatest. The mathematical representation of the atomic orbital predicts the presence of an electron in such a region.
Interesting Science Videos
What is Atomic Orbital?
An atomic orbital is a mathematical function that describes the wave-like behavior of either helps to determine the likelihood of discovering any atom’s electron in any particular area surrounding the nucleus. Additionally, the term could be used to describe the physical region where an electron can be calculated based on the orbital’s specific mathematical form.
The atomic orbital model is also referred as the electron cloud model or wave mechanics model. It is a contemporary framework for illustrating the microscopic behavior of electrons in matter. Atomic orbitals are its fundamental building blocks. According to this model, the electron configuration that forms the electron cloud of a multi-electron atom is essentially the result of simpler hydrogen-like atomic orbitals.
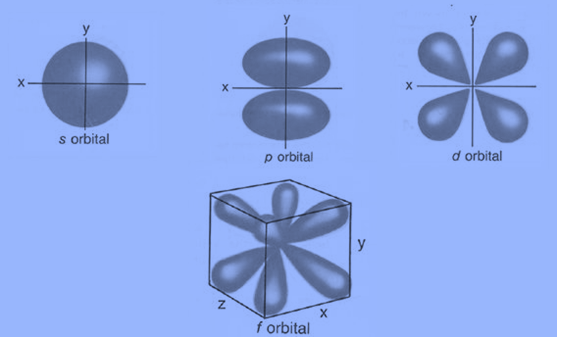
Quantum Numbers and Atomic Orbitals
- The electron’s energy, angular momentum, and an angular momentum vector component are all represented by the quantum numbers n, l, and m, which are used to classify atomic orbitals.
- Each orbital has a unique set of quantum numbers (n, l, and m) that define it and can hold up to two electrons, each with a unique spin quantum number.
- Simple names for orbitals with angular momentum quantum numbers l = 0, 1, 2, and 3 are the s orbital, p orbital, d orbital, and f orbital. Therefore, these names describe the electron configurations and denote the orbital shape.
The total number of electrons that occupy a full set of the s, p, d, and f atomic orbitals, respectively, naturally gives rise to the repeating periodicity of the blocks of 2, 6, 10, and 14 elements within sections of the periodic table.
History of Atomic Orbital
- Robert Mulliken coined the term “orbital” in 1932 as a shorthand for the one-electron orbital wave function.
- Around 1913, Niels Bohr provided an explanation of how electrons might spin around a compact nucleus with a fixed angular momentum.
- Bohr’s model was an improvement over Ernest Rutherford’s explanations from 1911, which described how an electron moved around a nucleus.
- Hantaro Nagaoka, a Japanese physicist, published an orbit-based explanation for electron behavior in 1904.
Each of these theories was developed from new observations, starting with simple understanding and progressing to more accurate and complex explanations. One of the factors that sparked the development of quantum mechanics was the need to explain the behavior of these electron “orbits.”
Orbits and Orbitals
An orbital is a likely area within an atom where the maximum density of electron presence can be found. In contrast, an orbit simply exists in a body of a certain mass. Whereas an orbital is present in an electron and an atom.
Orbit: An Orbit is a well-defined circular path around the nucleus along which electrons revolve. Another name for it is a shell.
It is indicated by the letter “n,” the primary quantum number. In order to move from one orbit to another, electrons must either absorb or release energy. Assume that an electron must release a certain amount of energy when it moves from a higher energy level to a lower energy level, and that it must absorb energy when it moves from a lower energy level to a higher energy level.
Orbital: An orbital is a region of uncertainty in which the presence or location of an electron is most likely. The area surrounding the nucleus is therefore a three-dimensional representation of the orbital. The energy of the orbital also makes it possible for it to have various shapes.
The Heisenberg Uncertainty Principle
According to the Heisenberg Uncertainty Principle, it is impossible to predict an electron’s position both now and in the future. This indicates that it is impossible to determine an electron’s position and momentum with absolute accuracy.
The orbitals depict the shape of the area where an electron will typically be found 95% of the time.
The exact position and exact velocity of any object in the universe cannot, even in theory, be calculated simultaneously, according to the Heisenberg uncertainty principle. However, we can quickly determine a car’s position and speed. This is because there is too little uncertainty in this situation.
As a result, the uncertainty principle only applies to tiny objects like atoms.
The momentum and position of a particle—whose momentum is equal to its mass times its velocity—are used in the uncertainty principle. The result of multiplying a particle’s momentum and position uncertainties is thus ≥ h/4pi. An unstable atom can also be described by this formula. Thus, there is no way to know with certainty where they will be in an atom.
Name of the Atomic Orbital
Each orbital in an atom is described by a unique combination of values for the three quantum numbers n (energy), l (angular momentum), and m (magnetic moment). A maximum of two electrons may be present in these orbitals. The orbitals with the values 0, 1, 2, and 3 for the angular momentum quantum number are the s-orbital, p-orbital, d-orbital, and f-orbital. These orbital names are used to describe the arrangement of an atom’s electrons, along with the energy quantum number (n).
For Example:
We plot the position of a hydrogen atom at a given instant. And then plot its position again after some time, we will discover that it is at a different position this time. If we keep doing it, the nucleus will eventually take on a spherical shape. The orbital that hydrogen occupies is designated as a 1-s orbital. Where “1” denotes the orbital’s energy level, which is closest to the nucleus, and “s” here denotes its spherical shape.
References
- Griffiths, David (1995). Introduction to Quantum Mechanics. Prentice Hall. pp. 190–191. ISBN 978-0-13-124405-4.
- Feynman, Richard; Leighton, Robert B.; Sands, Matthew (2006). The Feynman Lectures on Physics – The Definitive Edition, Vol 1 lect 6. Pearson PLC, Addison Wesley.
- https://en.wikipedia.org/wiki/Atomic_orbital
- https://byjus.com/chemistry/atomic-orbitals/
- https://alevelchemistry.co.uk/notes/atomic-orbital/
- https://byjus.com/chemistry/difference-between-orbit-and-orbitals/#:~:text=An%20orbit%20is%20the%20simple,in%20a%20three%2Ddimensional%20motion.&text=An%20orbital%20can%20be%20defined,most%20likely%20to%20be%20found.
- https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Electronic_Structure_of_Atoms _and_Molecules/Atomic_ Orbitals
