A Born-Haber cycle is often used to analyze the energy breakdown of the process by which an ionic compound is formed from its constituent components. A Born-Haber cycle is a specific application of Hess’s Law for ionic compounds. It lets us figure out the lattice enthalpy, which we can’t find through experiments. Lattice enthalpy or Lattice energy is the change in enthalpy that happens when one mole of an ionic lattice is made from one mole of gaseous ions at standard state conditions.
Interesting Science Videos
What is Born-Haber Cycle?
The born-Haber cycle is a cycle of enthalpy change of process that leads to the formation of a solid crystalline ionic compound from elemental atoms in their standard state and of the enthalpy of formation of the solid compound so that the net enthalpy becomes zero.
Max Born and Fritz Haber, two German physicists, proposed the Born-Haber cycle in 1919.
The lattice energy of a crystalline solid is the energy that holds the compounds cations and anions in their specified places. Lattice energy is also illustrated as the amount of energy needed to break down one mole of ionic solid into its gaseous ions, or the amount of energy released when one mole of gaseous ions forms a solid ionic complex. This lattice energy cannot be measured experimentally. The lattice energy may only be indirectly estimated using Hess’s heat summation equation.
For the solid ionic compound to form from the elemental state of the constituent atoms, the enthalpy of all processes necessary for the formation of the solid ionic compound must be calculated in a form cycle such that the total energy on summation is zero, in accordance with Hess’s law of heat summation.
Components of Born-Haber Cycle
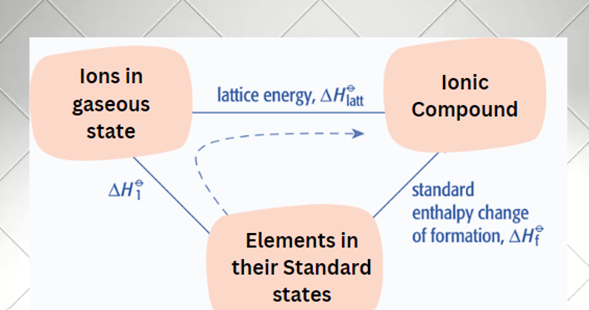
The dashed line represents the two-stage process: applying Hess’s law;
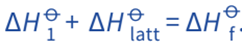
We can calculate the lattice energy of a compound if we know:
- its enthalpy changes of formation, ΔH
Of - the enthalpy changes involved in converting elements from their standard states to their gaseous ions, ΔH
O1
According to the Hess’s Law;
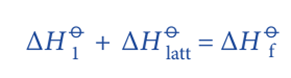
Rearranging the equation;
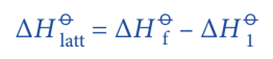
The enthalpy change (ΔHO1) involves several steps.
Calculating Lattice Energy or Lattice Enthalpy Using Born-Haber Cycle
The Born-Haber cycle uses enthalpy change to indirectly calculate the lattice energy of ionic compounds. It employs well-known thermodynamic variables like as ionization energy and electron affinity. Once a Born-Haber cycle has been formed, the lattice energy (ΔHꝋlatt) may be calculated using Hess’s formula.
Heat of Formation
The reaction between the elements in their normal states to generate the ionic compound is called formation. The heat of formation is the enthalpy change that occurs when a compound is formed from its constituent parts. Because ionic substances are stable, this value is usually negative. It also suggests that the formation process is exothermic.
Step 1: Sublimation and Dissociation Energy
The elements involved in the reaction must be in the gaseous state. Atomization is the process of forming gaseous atoms which gaseous atoms are formed from naturally existing elements. Metals exist in nature as single atoms. Nonmetals, on the other hand, exist in polyatomic form. As a result, energy is given to non-metals in order for them to dissociate into atoms.
Step 2: Electron Affinity and Ionization Energy
The removal of electrons from a gaseous state to generate a gaseous state is known as ionization. In order to do this, energy must be imparted to the gaseous atom. Ionization energy is the energy necessary to remove an electron from a neutral atom or ion. A gaseous nonmetal atom, on the other hand, releases energy when electrons are combined to create an ion. The energy generated when an electron is introduced to a neutral atom or an ion is referred to as electron affinity.
Step 3: Lattice Energy
Finally, the gaseous ions that make up the ionic compound are formed. We will calculate the lattice energy (ΔHꝋlatt) released during the crystallization of sodium chloride when the gaseous sodium ion and gaseous chloride ion combine to create a solid molecule.
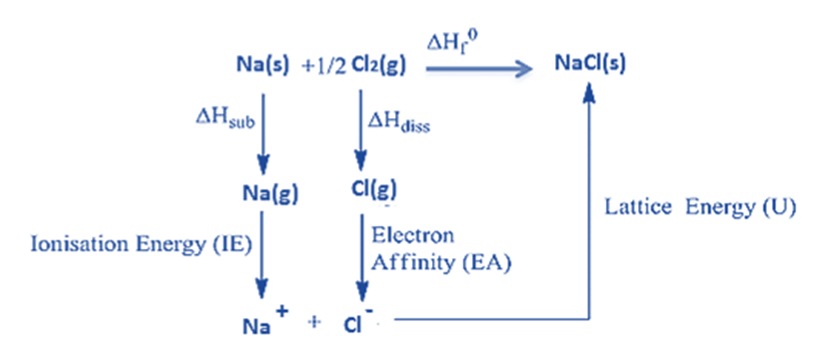
Lattice Energy Calculation of Sodium Chloride using Born-Haber Cycle
The Born-Haber cycle of sodium chloride (NaCl) is an example of an AB-type Monovalent ionic solid).
The heat of the formation of sodium chloride (ΔHOf) from sodium metal and chlorine gas can be measured experimentally.
Na (s) + (1/2) Cl2 (g) → NaCl (s) ΔHOf = -411kJ/mol
Ionic solid sodium chloride is made from solid sodium metal and gaseous chlorine. This is not a single-step process, but rather a series of steps. With the exception of the lattice energy, the heat changes of all the other processes may be observed experimentally.
In order to produce sodium chloride, the following procedures or actions must take place:
1: First, the solid sodium atom must absorb heat energy ( ΔHsub) to change into the gaseous sodium atom.
Na (s) → Na (g) ΔHsub = + 107 kJ/mol
2: The ionization energy is absorbed by the gaseous sodium atom, which then gives up an electron, forming a gaseous sodium ion.
Na (g) → Na+(g) + 1e– ∆HIE = +502 kJ/mol
3. Diatomic gaseous chlorine breaks into two separate atoms by absorbing bond energy, so that each chlorine atom absorbs half of the bond energy of a chlorine molecule.
Cl2 (g) → 2Cl (g) (1/2) ∆Hdiss= (1/2) * 242 = +121 kJ/mol
4. When a chloride ion is formed when a chlorine atom absorbs an electron, the resulting energy is equal to the ion’s electron affinity.
Cl(g) + 1e– → Cl– (g) ∆HEA = -355 kJ/mol
5. Energy equal to the lattice energy is released when a gaseous sodium ion and a gaseous chloride ion unite to create a solid sodium chloride molecule.
Na+(g) + Cl– (g) → Na+ Cl– (s)
When you add up the enthalpies of all the processes from step 1 to step 5, you get the net enthalpy of making solid crystalline sodium chloride from sodium and chlorine in their normal states, which are solid and gas, respectively. The enthalpy of production of solid sodium chloride has been determined experimentally, therefore this should be the same.
ΔHOf = ΔHsub + ∆HIE + (1/2) ∆Hdis + ∆HEA + U
ΔHOf – (ΔHsub + ∆HIE + (1/2) ∆Hdis + ∆HEA + U)=0
411 + 107 + 502 +121 -355 +U = 0
Here, except lattice energy, all other enthalpies can be experimentally measured.
Lattice energy of the sodium chloride solid (U)
= ΔHOf – (ΔHsub + ∆HIE + ½ ∆Hdis + ∆HEA).
= -411 -107 -502 -121 +355
= – 786 kJ/mol
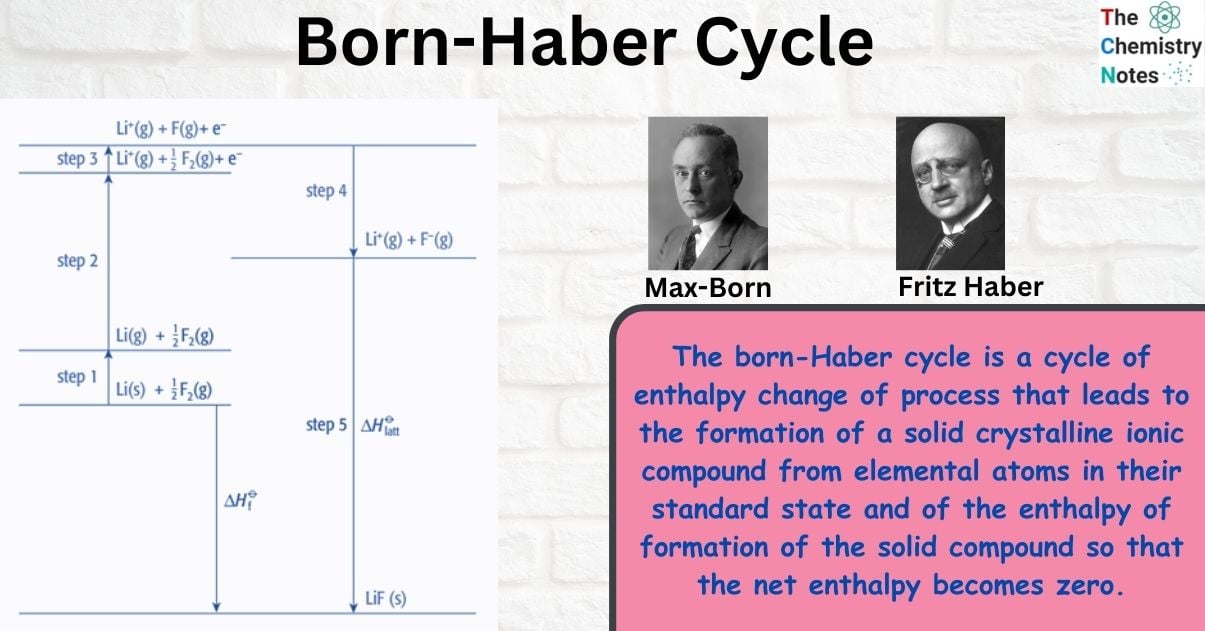
Born–Haber cycle as an energy level diagram
The Born-Haber cycle can be represented as an energy level diagram. This is the clearest and most effective form of Born–Haber cycle diagram.
Step 1: Start by putting the elements in their standard state on the left.
Step 2: Add the other enthalpy changes in the order of steps 1 to 4.
Step 3: Complete the cycle by adding the enthalpy change of formation and lattice energy.
Note that the arrows going upwards represent an increase in energy (ΔHO
is positive) and the arrows going downwards represent a decrease in energy (ΔHO
is negative)
Application of Born-Haber Cycle
- In order to explain why some compounds exist while others do not. It also determines how stable the compounds are.
- Estimating the affinities of electrons. From theoretical lattice energy, the Born-Haber cycle can be utilized to calculate the electron affinities of individual atoms. But atoms can only be given a rough idea of their first electron affinity. Calculating the second electron affinity is hard because of the way the anion and extra electrons repel each other.
- Estimating the enthalpy of formation.
For brief lesson about lattice energy, the energy associated with the formation of an ionic compound, and the Born-Haber cycle Watch the video.
References
- H. Heinz and U. W. Suter Journal of Physical Chemistry B 2004, 108, 18341-18352.
- Moore, Stanitski, and Jurs. Chemistry: The Molecular Science. 3rd edition. 2008
- https://byjus.com/jee/born-haber-cycle/
- Theodore Lawrence Brown, Eugene, H., Bursten, B. E., Murphy, C. J., Woodward, P. M., Stoltzfus, M. W., & Lufaso, M. W. (2018). Chemistry : the central science (14th ed.). Pearson.
- https://www.savemyexams.co.uk/a-level/chemistry/aqa/17/revision-notes/5-advanced-physical-chemistry-a-level-only/5-1-thermodynamics-a-level-only/5-1-2-born-haber-cycles/
- House, J. E., & Kathleen Ann House. (2016). Descriptive inorganic chemistry. Amsterdam ; Boston ; Heidelberg ; London ; New York ; Oxford ; Paris ; San Diego ; Singapore ; Sydney ; Tokyo Elsevier.
- https://chemistnotes.com/inorganic/born-haber-cycle-determination-of-lattice-energy/
- https://www.chemistrylearner.com/born-haber-cycle.html

