The Crystal Field Theory (CFT) is a concept for transition metal-ligand bonding interactions. It describes the attraction between the positive charge of the metal cation and the negative charge of the ligand’s non-bonding electrons. When the ligands approach the central metal ion, the static electric field produced by the surrounding charge distribution breaks the degeneracy of electronic orbital states, usually d or f orbitals. CFT can account for some magnetic properties, colors, and hydration energies of transition metal complexes, but it cannot describe bonding.
Interesting Science Videos
Crystal Field Theory
CFT explains- “the net change in crystal energy caused by the orientation of a transition metal cation’s d-orbitals within a coordinating group of anions known as ligands.”
This theory clarifies metal complex bonding, properties, electronic spectra, and magnetism.
The crystal field theory (CFT) was proposed by H. Bethe and V. Bleck.
The difference in color between two similar metal-ligand complexes is explained by crystal field splitting.
Crystal field splitting refers to the conversion of five degenerate d-orbitals of a metal ion into different sets of orbitals with different energies in the presence of a ligand crystal field. Crystal field splitting is the cornerstone of crystal field theory.
The difference in energy between ligand d orbitals is crystal field splitting. The capital Greek letter Δ denotes the crystal field splitting number.
Postulates of Crystal Field Theory
The postulates of CFT Theory are as follows:
- According to the crystal field theory, the metal ion is surrounded by an electric field caused by the ligands.
- The crystal field theory considers that the metal ion is situated in an electric field caused by the surrounding ligands.
- The attraction between the central metal and the ligand in a complex is purely electrostatic. The negative end of the dipole of the neutral molecule ligand is direct toward the metal ion.
- The transition metal or ion is a positive ion of charge equal to the oxidation state.
- the Definite number of ligands surrounds the transition metal atom or ion, it may be a negative ion or neutral molecule having lone pairs of electrons.
- The ligands are point charges and produce an electric field. This electric field changes the energy of the orbitals on the metal atom or ions.
- Due to the repulsive force between the central metal ion and ligand, the electrons on the metal ion occupy the d-orbitals as far as possible from the direction of approach of the ligand.
- There is no interaction between the metal orbital and ligand orbitals.
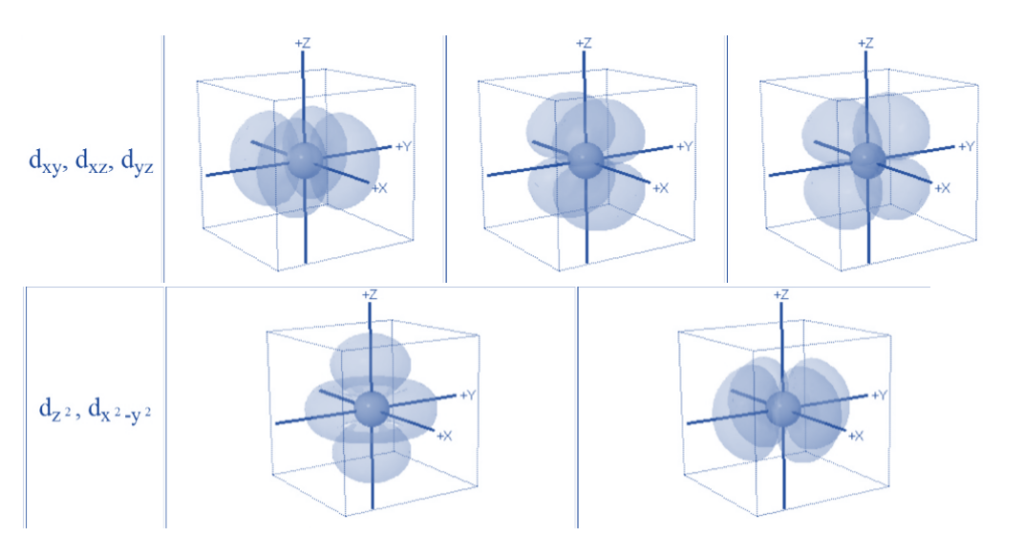
- In an isolated metal atom or ion, all the orbitals have the same energy, i.e., all five d orbitals (dxy, dxz, dyz, dx2–y2 and dz2) are degenerate.
- If the central metal atom or ion is surrounded by the spherical symmetrical field of negative charges, the d-orbitals remain degenerate. However, the energy of the orbitals is high due to the repulsion between the field and the electron on the metal atom or ion. In most transition metal complexes, the d-orbitals affects differently, and their degeneracy is loss due to the field produced by the unsymmetrical ligand.
Concept of Crystal Field Theory
The ions are assumed to be simple point charges in CFT. Bond energies are generally calculated successfully when applied to alkali metal ions with a symmetric sphere of charge. The method employed employs classical potential energy equations that account for attractive and repulsive interactions between charged particles (i.e., Coulomb’s Law interactions).
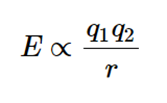
- E the bond energy between the charges and
- q1 and q2 are the charges of the interacting ions and
- r is the distance between them.
To clearly understand the crystal field interactions in transition metal complexes, knowledge of the geometrical or spatial disposition of d orbitals is necessary. In a free gaseous metal ion, the d-orbitals are five fold degenerate. If a spherically symmetric field of negative ligand filled charge is on a central metal ion, the d-orbitals remain degenerate but the energy of the free ion changes.
The metal-ligand bond also explains as an ionic bond arising solely from electrostatic interactions between metal ions and ligands by crystal field theory. Anions are as point charges in crystal field theory, while neutral molecules are as dipoles.
When transition metals aren’t bonded to anything, their d orbitals degenerate, which means they have the same energy. When they begin bonding with other ligands, the d orbitals split apart and become non-degenerate due to different symmetries of the d orbitals and the inductive effect of the ligands on the electrons.
Electrons in d-orbitals
The Aufbau principle states that electrons are filled from lower to higher energy orbitals This corresponds to the dxy, dxz, and dyz orbitals in the octahedral case. Electrons are filled in accordance with Hund’s rule in order to have the greatest number of unpaired electrons. There would be three unpaired electrons in a d3 complex, for example.
- If an electron is added, it can fill a higher energy orbital (dx2–y2 and dz2) or pair with an electron in the dxy, dxz, and dyz orbitals. This electron pairing necessitates the expenditure of energy (spin pairing energy).
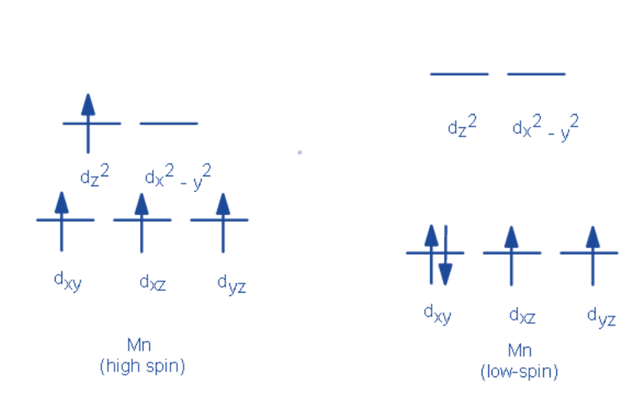
- If the pairing energy is less than the crystal field splitting energy, 0, the next electron will be stable and will enter the dxy, dxz, and dyz orbitals. This situation, known as low spin, allows for the fewest number of unpaired electrons.
- If the pairing energy is greater than zero, the next electron will be an unpaired electron in the dx2–y2 or dz2 orbitals. This situation, known as high spin, allows for the greatest number of unpaired electrons. Weak-field ligands are those that cause a transition metal to have a small crystal field splitting, resulting in high spin. Shortly, strong field ligands are those that cause a large crystal field splitting, resulting in a low spin.
Low spin and High spin
High-spin complexes are known for having a higher proportion of unpaired electrons, while low-spin complexes have a lower proportion. With weak field ligands, high spin complexes are expected because the crystal field splitting energy is low. The opposite is true for low spin complexes, where strong field ligands cause maximum electron pairing in the set of three t2 atomic orbitals due to large Δo.
High spin – Maximum number of unpaired electrons.
Low spin – Minimum number of unpaired electrons.
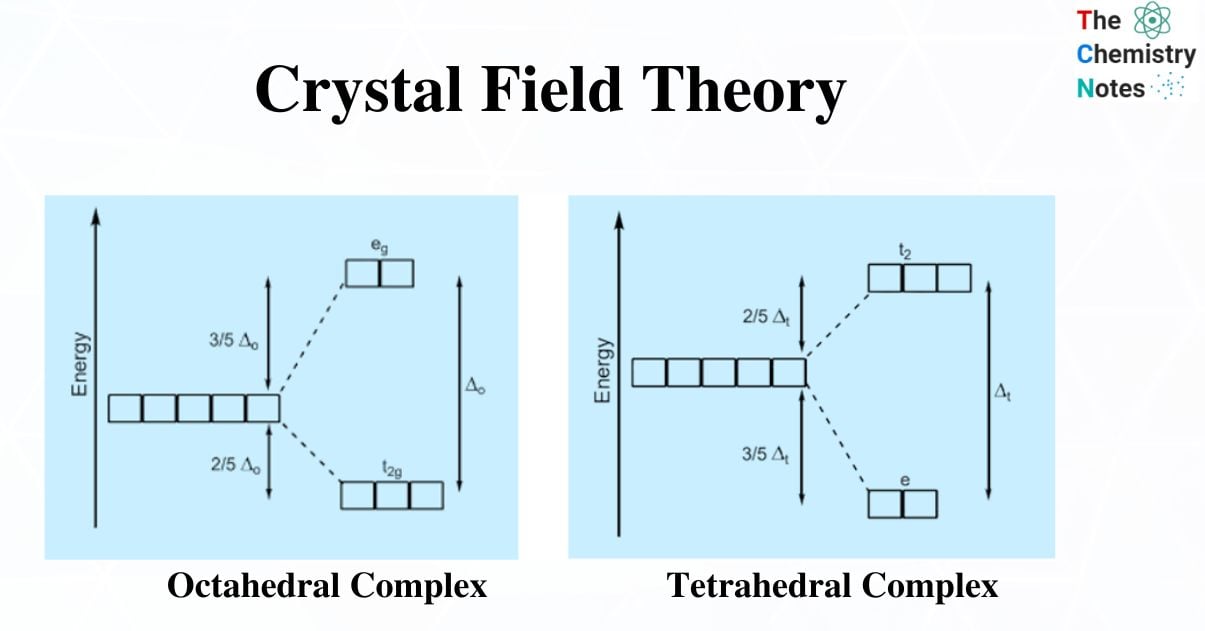
Crystal Field Splitting in an Octahedral Field
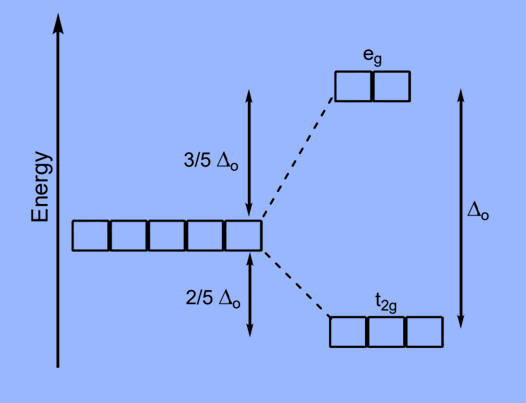
- In octahedral complexes, repulsion between the ligands and the d-orbitals occurs as the ligands approach metal ions,as a result raising their energy relative to the free ion. The ligands repel dx2–y2 and dz2 orbitals more strongly than the remaining three d-orbitals, dxy, dxz, and dyz.
- As a result, the energies of the dxy, dxz, and dyz orbitals are lower than the energies of the dx2–y2 and dz2 orbitals.
- Lower-energy dxy, dxz, and dyz orbitals are t2g orbitals, while higher-energy dx2–y2, dz2 orbitals are eg orbitals.
- The difference in energy between the two sets of d- orbitals is crystal field splitting energy or crystal field stabilization energy (CFSE). Specifically, the letter ΔO represents the octahedral complex.
- The eg orbitals have an energy level of +0.6 Δ0 or 3/5 Δ0 above the average, whereas the t2g orbitals have an energy level of –0.4 Δ0 or –2/5 Δ0 below the average.
- Strong field ligands have a high Δ0 value and thus are low spin complexes in octahedral complexes. [Fe(CN)6]4– and [Co(NH3)6]3+ are two examples.
- The weak field ligands are high spin complexes with a low Δ0 value.
Crystal Field Splitting in Tetrahedral Complex
- The representation of two sets of orbitals as Td is the splitting of fivefold degenerate d orbitals of the metal ion into two levels in a tetrahedral crystal field.
- The ligands repel electrons in dx2–y2 and dz2 orbitals less than electrons in dxy, dyz, and dxz orbitals.
- As a result, the energy of the dxy, dxz, and dyz. orbital sets increases while the energy of the dx2–y2 and dz2 orbitals decreases.
- Td complexes have only four ligands, so the total negative charge of four ligands, and thus the ligand field, is less than that of six ligands.
- The orbital orientation does not correspond to the ligands’ approaches to the metal ion.
- As a result, the repulsions in a tetrahedral coordination compound produce two energy levels:
t2– A group of three orbitals with higher energy (dxy, dxz, and dyz).
e – a pair of lower-energy orbitals ( dx2–y2 and dz2).
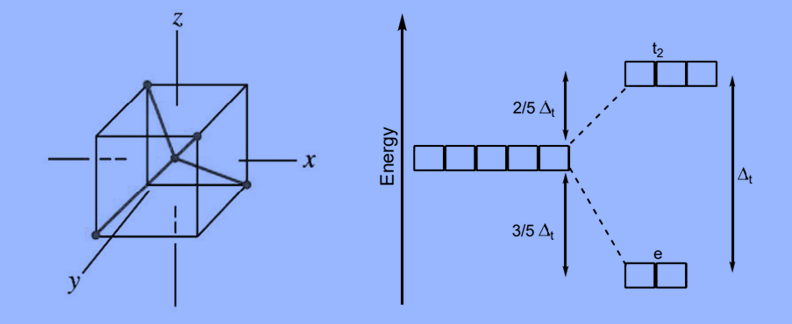
Because there are only two-thirds as many ligands in a tetrahedral complex and they have a less direct effect on the d orbitals, the crystal field splitting in a tetrahedral complex is intrinsically smaller than in an octahedral complex. The relative stabilizing effect of the e set is -6Dq, while the destabilizing effect of the t2 set is +4Dq.
Crystal Field Stabilization Energy
Crystal field splitting energy or crystal field stabilization energy is the difference in energy between the two sets of d-orbitals (CFSE). It is denoted by the symbol Δ.
The energy levels in a chemical environment generally split as directed by the symmetry of the local field surrounding the metal ion. The difference in energy between the eg and t2g levels is denoted by or 10Dq. It is stated that each electron that enters the lower t2g level stabilizes the system by -4Dq and each electron that enters the eg level destabilizes the system by +6Dq That is, the t2g is reduced by 4Dq while the eg level is increased by +6Dq.
As shown below, the net change in energy for d5 and d10 systems is zero.
d5: -12Dq + 12Dq = 0
d10: 6(-4Dq) + 4(+6Dq) = -24Dq + 24Dq = 0
| Total d-electrons | Octahedral | Tetrahedral | ||
| CFSE | CFSE | |||
| d0 | t2g0 | 0 Δo | e0 | 0 Δt |
| d1 | t2g1 | -2/5 Δo | e1 | -3/5 Δt |
| d2 | t2g2 | -4/5 Δo | e2 | -6/5 Δt |
| d3 | t2g3 | -6/5 Δo | e2t21 | -4/5 Δt |
| d4 | t2g3eg1 | -3/5 Δo | e2t22 | -2/5 Δt |
| d5 | t2g3eg2 | 0 Δo | e2t23 | 0 Δt |
| d6 | t2g4eg2 | -2/5 Δo + P | e3t23 | -3/5 Δt + P |
| d7 | t2g5eg2 | -4/5 Δo + 2P | e4t23 | -6/5 Δt + 2P |
| d8 | t2g6eg2 | -6/5 Δo + 3P | e4t24 | -4/5 Δt + 3P |
| d9 | t2g6eg3 | -3/5 Δo + 4P | e4t25 | -2/5 Δt + 4P |
| d10 | t2g6eg4 | 0 Δo | e4t26 | 0 Δt |
Factors Affecting the Magnitude of Orbital Splitting Energy (Δ)
- The higher the oxidation state of the central ion, the greater the value of orbital splitting energy.
- The d-block (transition) element value increases from 3d to 4d to 5d. As a result, elements in the second (4d) and third (5d) transition series are more likely than elements in the first (3d) transition series to form low-spin complexes.
- The value of the coordinating entity aids in complex classification. Particularly, the tetrahedral complex has roughly half the value of the octahedral complex.
Limitations of Crystal Field Theory
The majority of the properties of coordination complexes and the bonding between metal and ligand in the complex are explained by crystal field theory. It does, however, have some limitations. The following are the major limitations of this theory.
- Crystal field theory only considers a metal atom’s d orbital. However, in some cases, the contribution of s and p orbitals is considered.
- According to crystal field theory, metal-ligand bonding is purely electrostatic attraction. However, this is not the case.
- Moreover the covalent nature of the bond between the ligand and the central metal is not taken into account.
- The orbitals of ligands are not discussed in crystal field theory. It is significantly only focused on the metal orbital.
References
- Shriver, D. F.; Atkins, P. W. (2001). Inorganic Chemistry (4th ed.).
- https://chem.libretexts.org/Courses/Heartland_Community_College/HCC%3A_Chem_162/24%3A_Chemistry_of_Coordination_Compounds/24.7%3A_Crystal_Field_Theory_%E2%80%93_splitting_patterns_for_octahedral%2C_tetrahedral%2C_and_square_planar%3B_high_and_low_spin%2C_spectrochemical_series%2C_and_estimating_delta
- https://byjus.com/chemistry/crystal-field-theory/
- https://en.wikipedia.org/wiki/Crystal_field_theory
- https://www.coursehero.com/study-guides/introchem/crystal-field-theory/
- https://www.geeksforgeeks.org/crystal-field-theory/
- https://www.vedantu.com/chemistry/limitations-of-crystal-field-theory
- https://www.toppr.com/ask/en-np/content/concept/crystal-field-theory-203883/
