In thermodynamics, free energy is an energy-like characteristic or a state function of a system that is in thermodynamic equilibrium. How systems adapt and how much work they can produce are both determined by free energy. The Gibbs free energy G and the Helmholtz free energy F are the two ways in which it can be expressed.

Interesting Science Videos
Gibbs Free Energy
It is a unit of measurement used to determine the maximum amount of work that can be accomplished in a thermodynamic system when the temperature and pressure are held constant.
The other name of Gibbs free energy is Gibbs function, Gibbs energy, or free enthalpy. The symbol for Gibbs’s free energy is ‘G’. Typically, its value is in joules or kilojoules.
Gibbs’s free energy is the maximum amount of work that a closed system can extract. Gibbs free energy is a crucial quantity in thermodynamics that makes it possible to forecast certain aspects of a chemical reaction.
Gibbs free energy’s equation is:
G = H – TS
where G, H, T, and S represent the Gibbs free energy, enthalpy, temperature, and entropy, respectively.
American scientist Josiah Willard Gibbs developed Gibbs energy in the 1870s. He first referred to this energy as a system’s “available energy.” In his paper “Graphical Methods in the Thermodynamics of Fluids,” which was published in 1873, he explained how his equation could forecast how systems would behave when they are combined.
Equation for Gibbs free energy
We must take the overall entropy change in the universe into account in order to forecast the direction of spontaneous change.
S Universe = S Surroundings + S System
S Universe = q Surroundings / T + q System /T
The heat change in the system is equivalent to the opposite of the heat change in the surroundings, according to our definition of entropy:
q Surroundings / T = – q System / T
For a system that can perform work, we can write
q System = H
Now the change in the universe in the terms of changes in the system
q Surroundings / T = − H / T
The entropy then becomes;
S Universe = − H / T + S System
TS Universe = −H + TS System
−TS Universe = H − TS System
G = H − TS System
where G is the Gibbs function
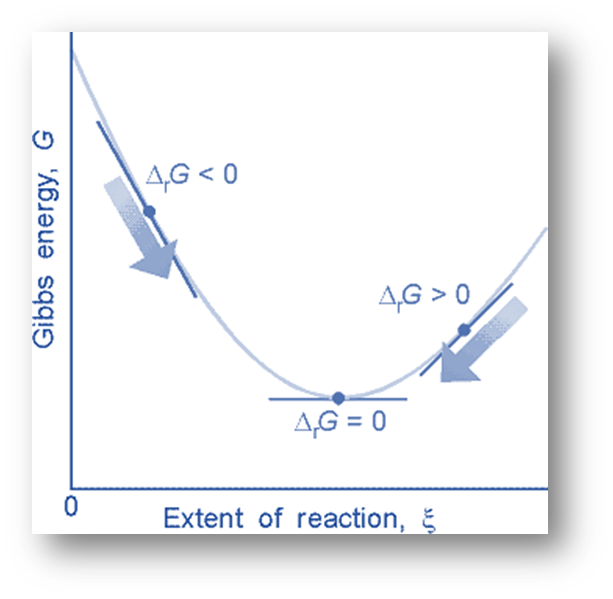
Feasible or Spontaneous Changes
Changes in the Gibbs free energy G correlate with changes in the free energy for processes that take place at constant pressure and temperature. The maximum non-expansion work possible in a closed system under these circumstances is represented by the change in Gibbs free energy.
The simple criteria for Gibbs function in terms of sign is:
- ∆G > 0 – Positive – Spontaneous
- ∆G = 0 – Equal – Equilibrium
- ∆G < 0 – Negative – Non-spontaneous
G is negative for spontaneous processes, positive for nonspontaneous processes, and zero for processes in equilibrium.
| ∆H | ∆S | ∆G | Spontaneity |
| – | + | – | Always spontaneous |
| + | + | + or – | Spontaneous at high T |
| – | – | + or – | Spontaneous at low T |
| + | – | + | Never spontaneous |
Helmholtz Free Energy
Helmholtz Free Energy is the “useful work” that a closed system can generate in conditions of constant volume and temperature. The work of a closed system with constant temperature and volume is measured using thermodynamic potential under the concept of Helmholtz free energy.
Helmholtz’s free energy is energy that can be converted into work at constant temperature and volume.
Equation for Helmholtz free energy
A = U – TS
where A, U, T, and S represent the Helmholtz free energy, internal energy, temperature, and entropy, respectively.
Hermann von Helmholtz, a German scientist, developed the concept and hence the name is forwarded in his honor. In 1882, he first introduced the idea of free energy in a lecture titled “On the thermodynamics of chemical processes.”
The International Union of Pure and Applied Chemistry (IUPAC) recommends using the symbol A and the name Helmholtz energy, which are from the German word Arbeit (work).
Mathematical Derivation
The first law of thermodynamics states that
dU = ∂Q – ∂W
where U is the internal energy, δQ is the energy added by heating and δW is the work done by the system. From the second law of thermodynamics, for a reversible process, we may say that;
δQ = TdS
Additionally, the work done δW = pdV in the case of a reversible change.
dU = TdS – pdV
Applying the product rule for differentiation to d (TS) = TdS + SdT, we have:
dU = d(TS) -SdT – pdV
and:
d (U – TS) = -SdT – pdV
From the definition of A = U – TS we can write;
dA = -SdT – pdV
Application of Helmholtz equation
- As a sum of an ideal gas and residual terms in the equation of state, the Helmholtz function precisely characterize pure fluids (such as industrial refrigerants).
- A type of artificial neural network called an auto-encoder efficiently encode data. The total cost of coding and the reconstructed code is determined in this case using Helmholtz energy.
- Research on explosives makes use of Helmholtz free energy because pressure changes are what trigger explosive reactions.
- Helmholtz free energy defines fundamental equations of pure substance states.
Relationship between Gibbs Free Energy and Helmholtz Free Energy
The relationship what separates Gibbs free energy from Helmholtz free energy is that:
While Helmholtz free energy is based on constant volume, Gibbs free energy is based on constant pressure.
The total work in the previous equation can be thought of as being less than the ideal maximum of W ≤ −ΔF. The entire procedure might be reversible, which would limit the case.
The system enters an equilibrium where no more work can be produced once the Helmholtz free energy reaches its minimum value. The least Helmholtz free energy at constant temperature is around 2870 kJ, which is essential for energy production in all living cells.
Within a container with solid walls, the Helmholtz Free Energy concept manifests itself. The entire process runs under constant pressure rather than at a constant temperature. Normal air pressure and a range of temperatures are present when a vegetable is growing in a garden.
Energy dimensions, also referred to as thermodynamic potentials, are specified in the system in order to preserve the integrity of thermodynamic laws in open systems. These formulas explain the overall work done in the system using references to Helmholtz and Gibbs free energy.
References
- https://collegedunia.com/exams/helmholtz-free-energy-significance-application-equation-physics-articleid-1254
- https://byjus.com/physics/helmholtz-free-energy/#:~:text=In%20thermodynamics%2C%20the%20Helmholtz%20free,system%20at%20a%20constant%20temperature.
- https://www.vedantu.com/physics/helmholtz-free-energy
- https://www.toppr.com/guides/physics/waves/helmholtz-free-energy/
- Aston, J. and Fritz, J.J., Thermodynamics and Statistical Mechanics, John Wiley and Sons, Inc., New York, 1959.
- Atkins, P.W. and Julio de Paulo, Atkins’ Physical Chemistry, Oxford University Press, UK, Indian Edition 9, 2011.
