Michaelis-Menten kinetics is a model of enzyme kinetics that describes the relationship between enzyme and substrate concentrations and the rate of an enzyme-catalyzed reaction. The Michaelis-Menten equation describes the relationship between substrate and enzyme concentrations and the rates of enzyme-catalyzed reactions.

Interesting Science Videos
What is Enzyme Kinetics?
Enzyme kinetics is the scientific study of the rates of enzyme-catalyzed processes and the mathematical analysis of those rates.
Activity, specific activity (activity per unit mass), and turnover number (activity per mole of enzyme) are three basic parameters for evaluating enzyme reactions. The turnover rate is proportional to the rate of reaction of a single enzyme molecule per second.
The field of enzyme kinetics investigates the relationship between the concentrations of substrates and the rates of enzyme-catalyzed processes. Enzyme reactions are not characterized by simple zero, first, or second-order chemical reaction relationships. Instead, the rate of the reaction slows down to a limiting or saturation value. The Michaelis-Menten equation, whose two characteristic constants are Vmax and KM, determines this behavior.
Michaelis-Menten Equation
The Michaelis-Menten equation describes the relationship between substrate and enzyme concentrations and the rates of enzyme-catalyzed reactions. Scientists Leonor Michaelis and Maud Leonora Menten developed this equation/model in the 20th century to explain the difference in the rate of chemical reaction catalyzed by enzymes. Thus, the Michaelis-Menten equation is named after German biochemist Leonor Michaelis and Canadian physician Maud Menten.
It is an equation that relates reaction velocity to substrate concentration for a system in which a substrate S binds reversibly to an enzyme E to create an enzyme-substrate complex ES, which subsequently reacts irreversibly to generate a product P and regenerate the free enzyme E. This mechanism can be illustrated schematically as follows:
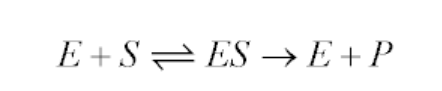
The Michaelis-Menten equation for this system is:
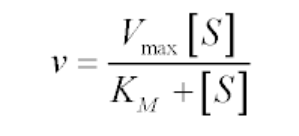
The Michaelis-Menten kinetics equation includes two key terms:
- Maximum reaction rate, or Vmax, occurs when all substrate binding sites in an enzyme are full.
- Michaelis constant or Km, is the concentration of substrate at which the reaction rate is half of its maximum value (Vmax). The Km value indicates how well an enzyme is able to perform its activity at different concentrations of its substrate; a lower Km value indicates better performance.
Assumptions of Michaelis-Menten Equation
The following key characteristics of several enzymes that catalyze reactions are taken into account when constructing the Michaelis Menten equation. It’s important to understand the key factors that were taken into making the Michaelis-Menten equation. This makes it possible to determine when the equation can be utilized and when it cannot.
- The initial rate of product formation is proportional to the total concentration of enzyme [E]o for a given initial concentration of substrate [S]o.
- In the context of low substrate concentrations, it can be observed that the rate of product formation exhibits a linear relationship with the substrate concentration, denoted as [S]o. This implies that the rate is directly proportional to the substrate concentration.
- Another assumption of the Michaelis-Menten model is that the concentration of the enzyme-substrate complex [ES] is constant. This is referred to as steady-state approximation.
- At a high concentration of substrate, the rate of product formation becomes independent of substrate concentration and reaches a maximum velocity, Vmax, at which substrate concentration has no effect.
- The substrate concentration [S] is approximately equal to the total substrate concentration. Technically, the total substrate concentration in the solution is equal to the sum of the concentrations of substrate [S] and enzyme-substrate complex [ES]. However, given that [S]>>>[E], the substrate concentration [S] is about equal to the total substrate concentration. This is referred to as free ligand approximation.
Derivation of Michaelis-Menten Equation
The equation arises from the general equation for an enzymatic reaction.
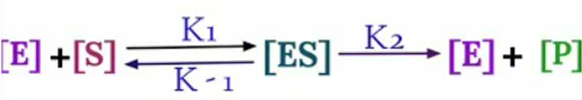
During Initial
Rate of Formation of [ES] = Rate of Breakdown of [ES]
K1 [E][S] = K-1 [ES]
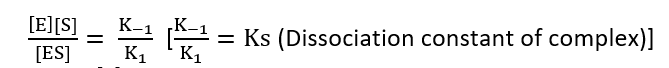
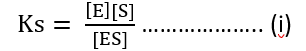
Total enzymes = E0
[E0] = [E] + [ES]
[E] = [E0] – [ES]
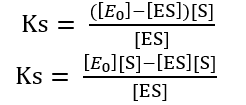
Ks [ES] + [ES][S] = [E0] [S]
[ES] (Ks + [S]) = [E0] [S]
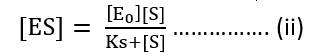
Now, velocity of reaction from [ES] to Product
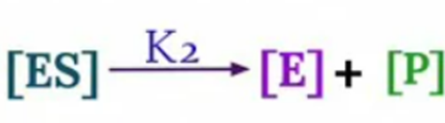
V0 = K2 [ES]
Substituting value of [ES] from equation (ii)
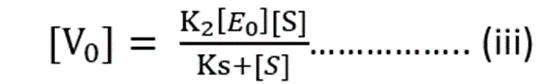
Maximum Rate of Reaction = Vmax
Vmax = K2 [E0] ……………. (iv)
Substituting value of equation (iv) into (iii)
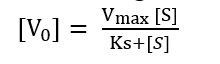
This is Michaelis-Menten equation
Alternative Approach





This is Michaelis-Menten equation
Graphical representation of Michaelis-Menten equation
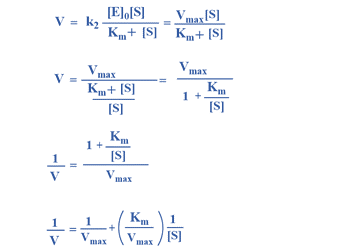
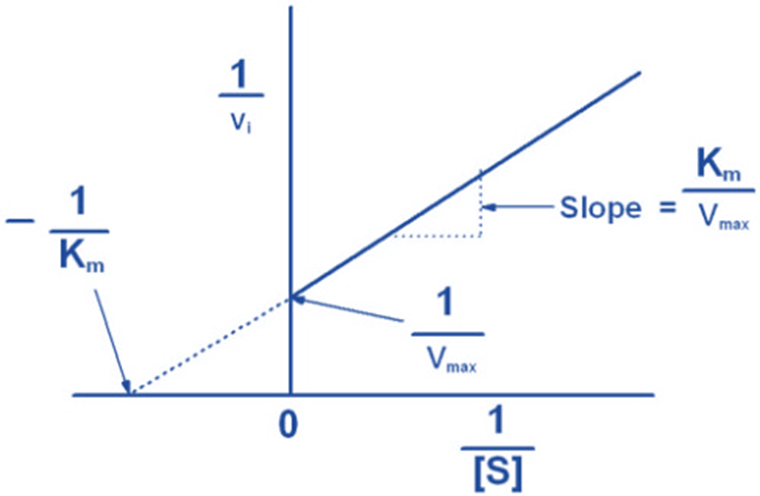
References
- https://www.maxbrainchemistry.com/p/michaelis-menten-equation.html
- https://www.tutorhelpdesk.com/homeworkhelp/Biochemistry-/Enzyme-Kinetics-Assignment-Help.html
- https://chelseaharripersad.wordpress.com/tag/michaelis-menten-equation/
- https://chemistnotes.com/physical/michaelis-menten-equation-assumptions-derivation-graphs/
- https://teachmephysiology.com/biochemistry/molecules-and-signalling/enzyme-kinetics/
- https://chemistry.stackexchange.com/questions/4911/michaelis-menten-derivation-for-2-enzyme-substrates
- https://www.chem.ucla.edu/~rebecca/153A/MMkinetics.pdf
- Lehninger A.B.,(2018), Textbook of Biochemistry, Ed.5, Pearson International,
New York - Voet, D Voet, J.G. and Pratt, C.W.2013. Fundamentals of Biochemistry: Life at
molecular level
