Osmotic pressure is a ‘colligative’ property, similar to freezing point depression, meaning that it is influenced by the number of particles in a solution rather than their chemical composition. Osmosis is the movement of a fluid through a semipermeable membrane under the influence of a concentration gradient. A solution’s osmotic pressure is the pressure difference required to stop the passage of solvent across a semipermeable barrier. The osmotic pressure of a solution is proportional to the molar concentration of solute particles in solution.
Interesting Science Videos
What is Osmotic Pressure?
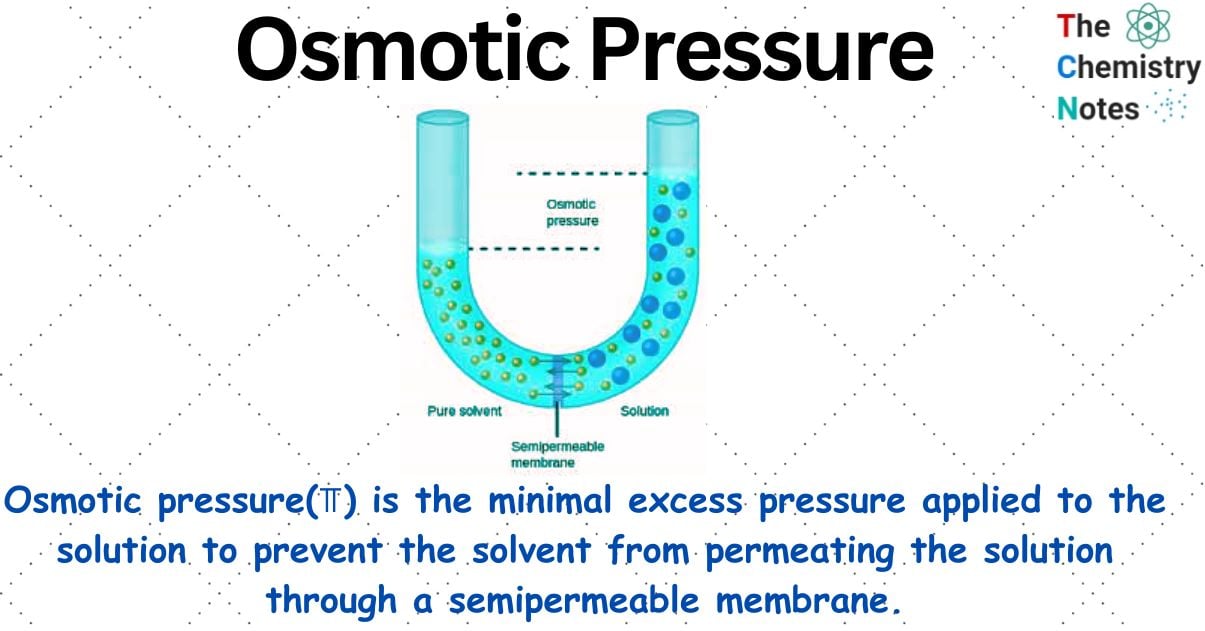
Osmotic pressure is the minimal excess pressure applied to the solution to prevent the solvent from permeating the solution through a semipermeable membrane. Osmotic Pressure is denoted by (⫪).
It has been discovered that when a semipermeable membrane is positioned between a solvent and a solution, solvent molecules pass through the barrier into the solution, increasing the volume of the solution. Only solvent molecules can pass across the semi-permeable membrane, however; solute and other larger molecules cannot.
Osmosis is the term used to describe the spontaneous movement of solvent molecules through a semipermeable membrane from a pure solvent to a solution or from a dilute to a concentrated solution.
Osmotic Pressure Formula
Dutch chemist Jacobus Henricus van’t Hoff discovered that the osmotic pressure of a diluted solution (⫪) obeyed a formula similar to the equation for an ideal gas.
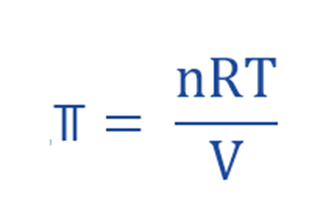
Where;
- ⫪ = Osmotic Pressure
- R = Universal gas constant (0.0821 L atm mol–1 K–1)
- T = absolute Temperature (in Kelvin)
- V = volume
- n = number of moles of solute in the solution
- (n/V) = Molar Concentration
Since osmotic pressure is directly proportional to the number of moles of the solute, it thus follows the definition of colligative property. Hence, we can say that it is considered a colligative property.
Laws of Osmotic Pressure
Van’t Hoff established the laws of osmotic pressure which are based on the experimental observations in 1877. These laws closely resembles the gas laws.
Boyle-van’t Hoff Law for Solutions
This relationship is also known as the Boyle-van’t Hoff law for solutions because it is comparable to Boyle’s law for gases.
The osmotic pressure (π) of a solution is directly proportional to the molar concentration of the solute at a constant temperature.
Mathematically, π ∝ C at Constant temperature
When 1 mole of solute is dissolved in 1 litre of solution, then concentration is measured in moles per litre;

Charles-van’t Hoff Law for Solutions
This relationship, which is also known as the Charles-van’t Hoff law for solutions, which is comparable to Charles’ Law for gases.
The osmotic pressure of a solution of given concentration varies directly as the temperature in Kelvin (K).
Mathematically, π ∝ T, at constant concentration.
Van’t Hoff Equation for Solutions
From Boyle-van’t Hoff law: π ∝ C
From Charles-van’t Hoff law for solutions: π ∝ T
Combining these two laws, we get;
π ∝ CT
π = RCT
π = (n/V) RT [Since, C = n/V i.e. number of moles per unit volume]
πV = nRT
Hence, the above equation is known as Van’t Hoff Equation for dilute solutions when n moles of solute are dissolved in V litre of solution.
The value of R computed from the experimental values of, V, and T came out to be roughly the same as of the Gas constant, R, which he used to demonstrate how this equation was parallel to the general Gas Equation (PV = RT).
For 1 mol of solute, the equation can be written as;
πV = RT
Avogadro-Van’t Hoff Law for Solution
For two different dilute solutions, Van’t Hoff equation for these solution can be written as;
For solution 1: π1.V1 = n1 R T1
For solution 2: π2.V2 = n2 R T2
If T1 = T2 and π1 = π2 , dividing above equation of two solutions, we get;
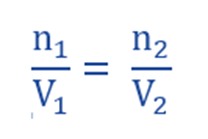
If the volume of two solutions is equal, then they contain equal number of moles.
Avogadro-Van’t Hoff Law for Solution is analogous to Avogadro’s Law.
Determination of Molecular Weight from Osmotic Pressure
Osmotic pressure measurements are less accurate and more complex to perform. As a result, this method is not extensively employed in the estimation of molecular weights. The main application of this method is to determine the molecular weights of polymers with very large molecular weights, such as plastics, proteins, and starch.
Knowing the osmotic pressure of a given solution, the molecular weight of the solute can be determined using the van’t Hoff equation.
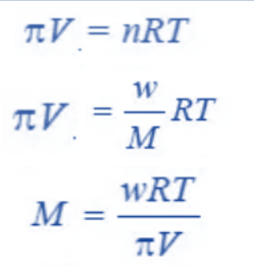
Where;
M = Molecular weight of the solute
w = weight of solute in grams
π = Osmotic Pressure in atmospheres
V = Volume of solution in litres
R = 0.0821 litre-atmosphere
T = Absolute Temperature
Experimental Determination of Osmotic Pressure
Pfeffer’s Method
The device used by Pfeffer (1877) to measure osmotic pressure is shown below. It is made up of a porous pot with a glass top attached to it and walls lined with copper ferrocyanide membrane. A closed mercury manometer and an open tube are both on the glass top’s side. Through the tube, which is then sealed off, the apparatus is filled with the solution being tested. Now the pot is submerged in pure water that is kept at a constant temperature. Water enters the solution through the membrane, creating pressure on the manometer in the process.
The osmotic pressure of the fluid is determined by the highest pressure the manometer records.
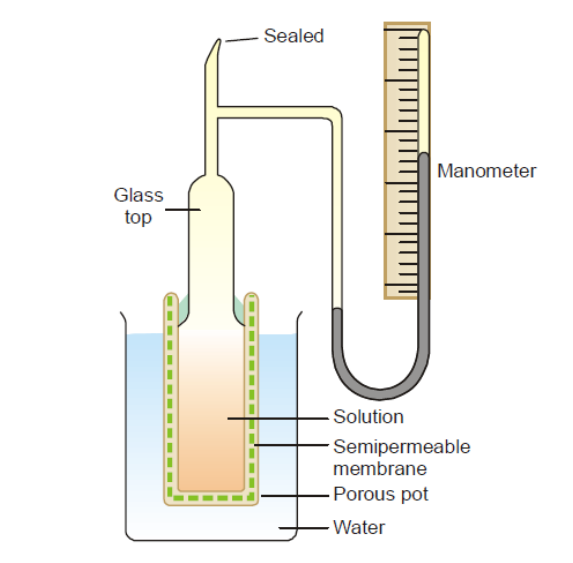
The Pfeffer’s approach has two drawbacks:
- It is slow and takes several days to attain the highest pressure.
- Because the ferrocyanide membrane is fragile, it cannot be utilized to measure high osmotic pressures.
Berkeley and Hartley’s method
The method of Berkeley and Hartley is the most commonly used method for determining the osmotic pressure of a solution. This method’s apparatus is depicted below.
The apparatus is made up of a porous tube carrying a semi-permeable copper Ferrocyanide membrane. It has a reservoir ‘R’ on one end and a capillary tube ‘M’ on the other end to display the level of solvent. The solvent is in the tube. This tube is housed in a gunmetal outer vessel and is equipped with a piston ‘P’ and a pressure gauge.
It is filled with a solution whose osmotic pressure is to be determined. As soon as osmosis begins, the level of solution rises and piston ‘P’ rises. Then additional weights are placed on the piston, which is sufficient to stop the osmosis and the level of the solvent remains steady in capillary tube ‘M’.
The pressure reported by the pressure gauge is thus the solution’s Osmotic pressure.
![Berkeley and Hartley’s method for determination of osmotic pressure [Image Source: gkscientist.com]](https://scienceinfo.com/wp-content/uploads/2023/05/image-28.png)
This method is better to the more traditional pfeffer method
- The measurement of high osmotic pressures is possible
- There is no strain left on the membrane and there is no risk of its rupture because the osmotic pressure is balanced by the external pressure.
A Modern Osmometer
A modern equipment for determining osmotic pressure is shown below.
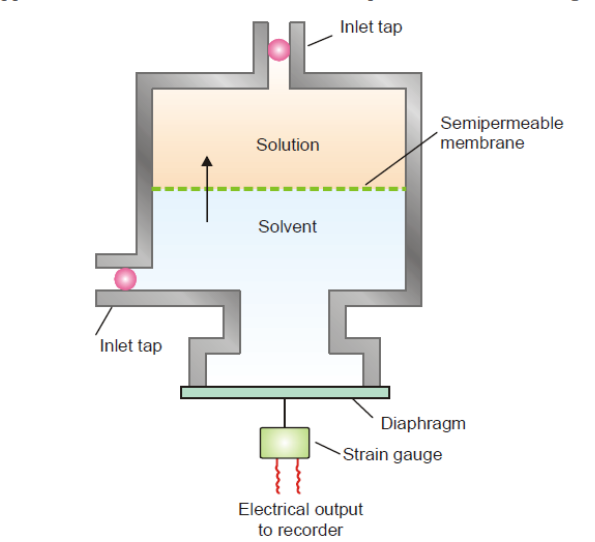
It comprises of a cell made of stainless steel with a fixed, stiff membrane that is semipermeable. The membrane creates compartments for the solute and solvent in the cell. The solvent compartment is then joined with the diaphragm after a solution under examination is added to the upper chamber. Osmosis allows the solvent to move from an area of lower concentration to one of higher concentration. A tool known as a strain gauge can be used to measure the strain that is applied to the diaphragm.
As a result, the strain generated is inversely proportional to the osmotic pressure. The electronic device to which the strain gauge is connected generates a digital signal in response. Consequently, the osmotic pressure is measured.
References
- Atkins, Peter and de Paula, Julio. Physical Chemistry for the Life Sciences. New York, N.Y.: W. H. Freeman Company, 2006. (124-136).
- McQuarrie, Donald, et al. Colligative properties of Solutions” General Chemistry Mill Valley: Library of Congress, 2011. ISBN 978-1-89138-960-3.
- Laidler, K.J.; Meiser, J.L. (1982). Physical Chemistry. Benjamin/Cummings. ISBN 978-0618123414
- https://qsstudy.com/determination-osmotic-pressure-pfeffer-s-method/
- https://readchemistry.com/2022/09/17/determination-of-osmotic-pressure/
- https://psiberg.com/osmotic-pressure/
- https://gkscientist.com/experimental-measurement-of-osmotic-pressure/
- https://readchemistry.com/2022/09/21/laws-of-osmotic-pressure/
