The Pauli Exclusion Principle helps us understand the electron arrangements in atoms and molecules. It also explains the classification of elements in the periodic table. Wolfgang Pauli, an Austrian physicist, first proposed the idea in 1925 for electrons and extended it to all fermions with his spin-statistics theorem in 1940. Wolfgang Pauli received the 1945 Nobel Prize in Physics for his discovery as it applied to electrons.

Interesting Science Videos
What is Pauli Exclusion Principle?
According to the Pauli Exclusion Principle, two electrons within an atom can’t possess identical sets of four electronic quantum numbers. Every electron must have different quantum numbers.
So, in each electronics orbital (same n, l, and ml) there can be two electrons and they must have different spins. The ms values of two electrons will be ms = + 1/2 and ms = – 1/2. Therefore, no two electrons will have the same four quantum numbers.
There are two salient rules that the Pauli exclusion principle follows:
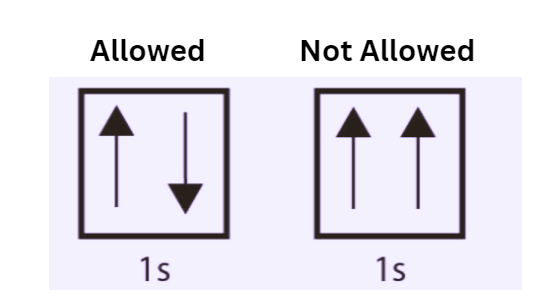
- Only two electrons can occupy the same orbital.
- The two electrons that are present in the same orbital must have opposite electronic spins, or they should be antiparallel.
Statement: It is impossible for any two electrons of an atom to have identical set of four quantum numbers.
The Pauli exclusion principle is not limited to electrons, but rather extends to fermions and other half-integer spin particles. Particles with an integer spin, such as bosons, possess symmetric wave functions, rendering the aforementioned statement irrelevant. In addition, it is noteworthy that bosons possess the capability to share or occupy identical quantum states, which is not a characteristic exhibited by fermions. Regarding the terminology, fermions derive their name from the Fermi-Dirac statistical distribution which governs their behavior. In contrast, bosons derive their nomenclature from the Bose-Einstein distribution function.
Four Quantum Numbers
Every electron in an atom can be defined by four quantum numbers that are:
(i) n: the principal quantum number
(ii) l: the orbital angular momentum quantum number
(iii) ml: the magnetic quantum number
(iv) ms: the spin quantum number
According to the Pauli’s Exclusion principle,
Any two electrons present in an atom can have an identical set of up to any three types of quantum numbers (n, l, ml, and ms), but the fourth one is never identical; otherwise, the electronic configuration becomes wrong. In simple terms, every electron should have or be in its unique state (the singlet state).
Therefore, the exclusion principle helps us to identify the wrong and right electronic configuration of an atom.For Example consider Li atom which has 3e– to be arranged properly. let us assume the following configuration.
(i) 1s3 ( wrong configuration)
(ii) 1s2, 2s1,…etc. ( Correct configuration)
Let us understand why (i) is the wrong configuration:
1s3 is the wrong electronic configuration of Li, and it is explained by assigning the values of quantum numbers for each as,
| orbit | n | l | m | s |
|---|---|---|---|---|
| 1st e– | 1 | 0 | 0 | +(1/2) |
| 2nd e– | 1 | 0 | 0 | -(1/2) |
| 3rd e– | 1 | 0 | 0 | +(1/2) |
Let us understand why (ii) is the correct configuration:
1s2, 2s1 is the correct configuration and it is explained similarly as follows:
| orbit | n | l | m | s |
|---|---|---|---|---|
| 1st e– | 1 | 0 | 0 | +(1/2) |
| 2nd e– | 1 | 0 | 0 | -(1/2) |
| 3rd e– | 2 | 0 | 0 | +(1/2) |
- No two electrons are found to have identical set of four quantum numbers and so 1s2,2s1 is the accurate electronic configuration of Li.
- The Pauli exclusion principle introduced the spin quantum number (ms) as a supplementary component to the three pre-existing quantum numbers (n, l, ml).
- A magnetic moment that is positive typically signifies a state of spin up and is conventionally denoted by an upward-facing arrow.
A negative millisecond value typically denotes a deceleration in rotational speed and is conventionally denoted by a downward-pointing arrow symbol.
The spin quantum number exhibits a unique characteristic in that it remains independent of the other quantum numbers. The possible values of the quantum number in question are restricted to + ½ or – ½, and these values are found to be uncorrelated with any other quantum numbers. The interconnection among the various quantum numbers is evident.
Pauli Exclusion Principle Examples
A neutral helium atom can serve as an illustration of the mutual Pauli Exclusion Principle.
- The atom possesses a pair of valence electrons that occupy the outermost shell and exhibit opposite spin orientations.
- It has been determined that the two electrons are located within the 1s subshell, characterized by the quantum numbers n = 1, l = 0, and ml = 0.
- The diversity of their spin flashes will also be apparent. One of the values is ms = -1/2, while the remaining values are +1/2.
- Upon diagrammatic representation, the subshell of the helium atom can be identified by the presence of one upper electron and one lower electron. The 1s subshell is theoretically capable of accommodating a maximum of two electrons, each possessing opposite spins.
- Similarly, in the case of Hydrogen, its electronic configuration comprises of a single 1s subshell with one valence electron (1s1). The atomic structure of lithium consists of a helium core (1s2) and an additional valence electron occupying the 2s orbital (2s1).
It is then concluded that an orbital can accommodate 2e– at maximum with the opposite electronic spin. This information can help determine the maximum number of electrons present in the subshells and shells of an atom. For example, consider the second shell (L shell), and the maximum accommodation of electrons in it is obtained from the following principle:
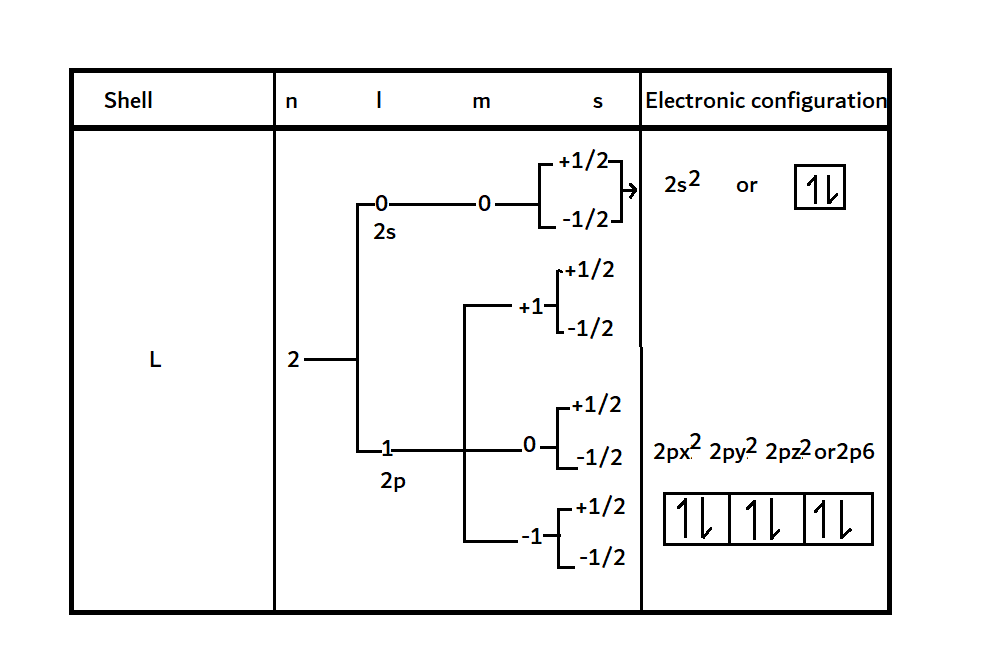
Therefore, the electronic configuration of the second shell of an atom obtained based on the exclusion principle is 2s2 2p6, and it contains 8e– at maximum. Hence, s, p, d, and f subshells can accommodate a maximum of 2, 6, 10, and 14 e–, respectively.
This principle is called the exclusion principle because the set of quantum numbers assigned to a particular electron of an atom is excluded from other electrons in the atom.
Importance and Application of Pauli Exclusion Principle
- The arrangement of elements in the periodic table can be simply explained by the Pauli Exclusion Principle, which states that no two electrons within an atom can possess identical quantum numbers.
- The Pauli Exclusion Principle dictates that the presence of two electrons in a given material occupying the same energy state is prohibited. The comprehension of Fermi levels within the solid-state band theory can be enhanced through the utilization of Pauli’s exclusion principle.
- The solid-state properties of various materials are influenced by the Pauli exclusion principle, which directly affects their electrical, optical, magnetic, mechanical, and chemical characteristics. The Pauli exclusion principle is a fundamental concept in physics that elucidates various physical phenomena, including the arrangement of electrons in the electron shells of atoms and the mechanism by which atoms share electrons.
- The exclusion principle formulated by Pauli pertains to the configuration of electrons within the elements.
- This facilitates the depiction of various chemical elements and their corresponding chemical bonds.
If you want to learn more about the origin of the Pauli exclusion principle, watch out for what causes the Pauli Exclusion.
Video on Pauli Exclusion Principle
References
- https://chemistrytalk.org/pauli-exclusion-principle/
- https://www.chemicool.com/definition/pauli-exclusion-principle.html
- https://byjus.com/jee/pauli-exclusion-principle/
- Liboff, Richard L. (2002). Introductory Quantum Mechanics. Addison-Wesley. ISBN 0-8053-8714-5.
- Massimi, Michela (2005). Pauli’s Exclusion Principle. Cambridge University Press. ISBN 0-521-83911-4.
- Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.). W. H. Freeman. ISBN 0-7167-4345-0
- https://www.sciencedirect.com/topics/pharmacology- toxicology-and-pharmaceutical-science/ pauli-exclusion-principle#
- https://unacademy.com/content/upsc/study-material/chemistry/a-brief-note-on-importance-and-application-of-paulis-exclusion-principle/

