The three-dimensional structures of organic compounds can be represented by different projections. Common Projections of organic compounds include Fischer projection, Sawhorse projection, and Newman projection.
Interesting Science Videos
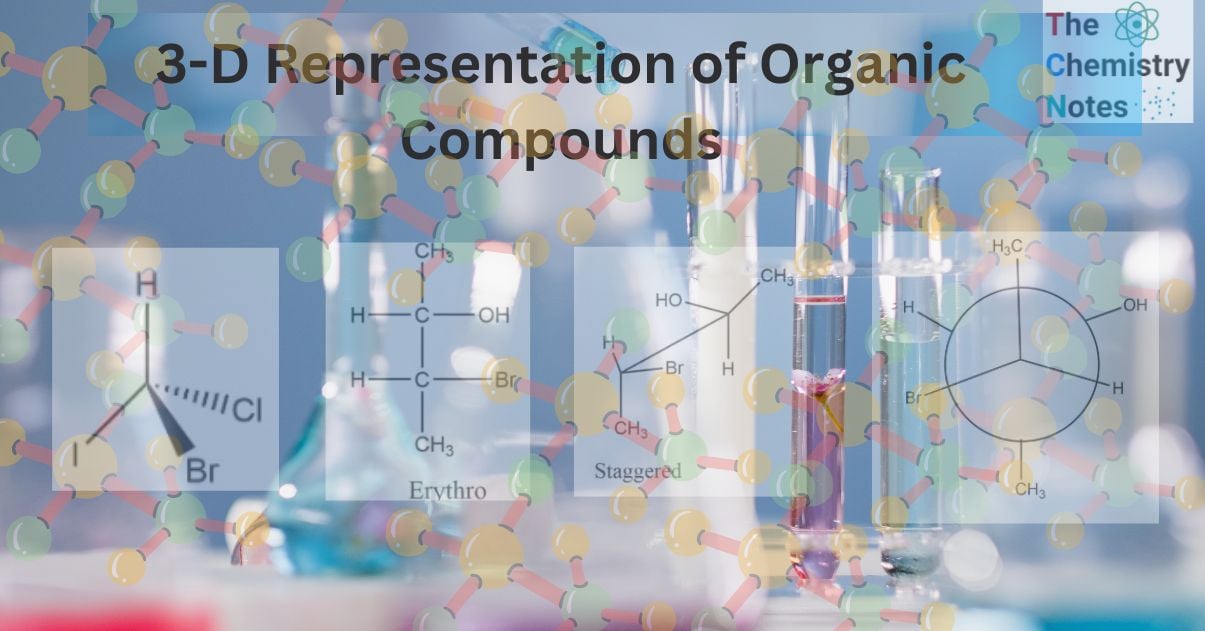
Flying Wedge or Wedge Dash projections of organic compounds
The Flying-Wedge Projection is the most common three-dimensional representation of a molecule on a two-dimensional surface. These representations are typically used for molecules with chiral centers. Three different types of lines are utilized in this type of representation.
- Solid wedges or thick lines (
 ) signify bond projections toward the observer or above the paper’s surface.
) signify bond projections toward the observer or above the paper’s surface.
- A continuous or regular line (
 ) denotes a bond in the paper’s plane.
) denotes a bond in the paper’s plane. - A dashed wedge or broken line (
 ) denotes bond projection below the plane of the paper or away from the observer.
) denotes bond projection below the plane of the paper or away from the observer.
For example:
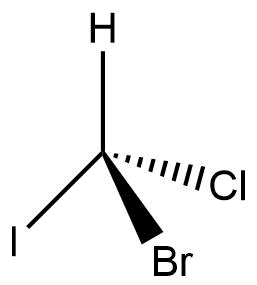
Fischer projection of organic compounds
The compound’s carbon chain is projected vertically, with the topmost carbon being the one that has undergone the most oxidation.
- Since it is in the plane of the paper, the chiral carbon atom is typically ignored.
- Crossed lines generally represent asymmetric carbon.
- The chiral carbon’s horizontal bonds are seen as being above the plane of the paper or pointing towards the observer.
- The chiral carbon’s vertical bonds are regarded as being below the plane of the paper or pointing away from the viewer.
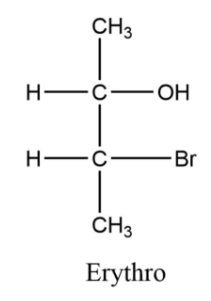
Fisher transformation of organic compounds
Emil Fischer demonstrated through experimentation that the enantiomers of optically active compounds of the type Cabde were obtained from the exchange of any two groups. This is known as the Fischer transformation.
The compounds a and b are enantiomers that can be explained using their models. This experiment demonstrates that it is feasible to convert a molecule into its enantiomer by changing the relative positions of two groups. As a result, this transition is referred to as the Fischer transition.
Applications of Fischer transformation
It is an effective method for manipulating formulas. Constructing the models, for instance, can help you determine whether the compounds a and b below are enantiomers or identical to one another.
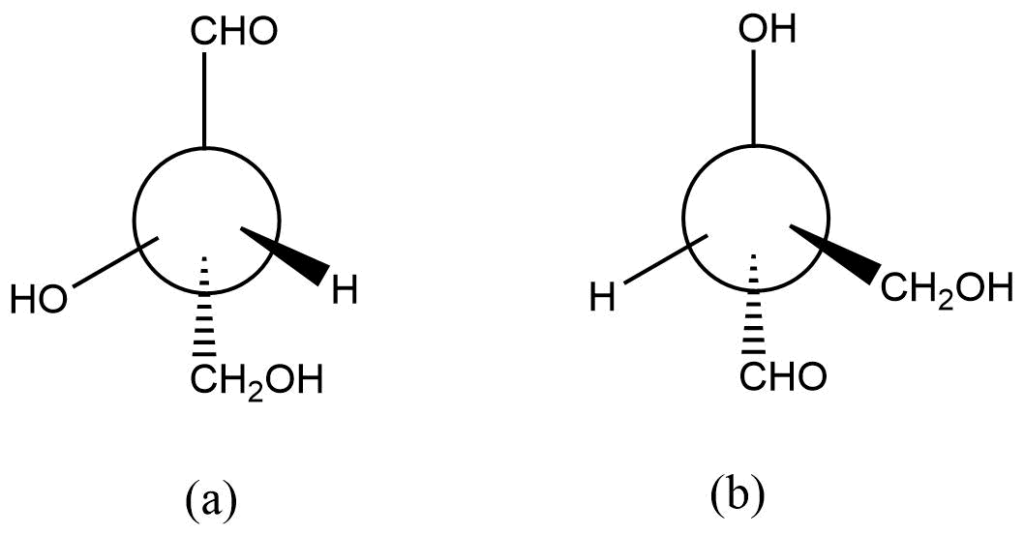
However, constructing a model is not always feasible or convenient. Although the phenomenon is complicated, it may also be described by utilizing three-dimensional projections. The Fischer transformation provides a straightforward way to respond to this problem.
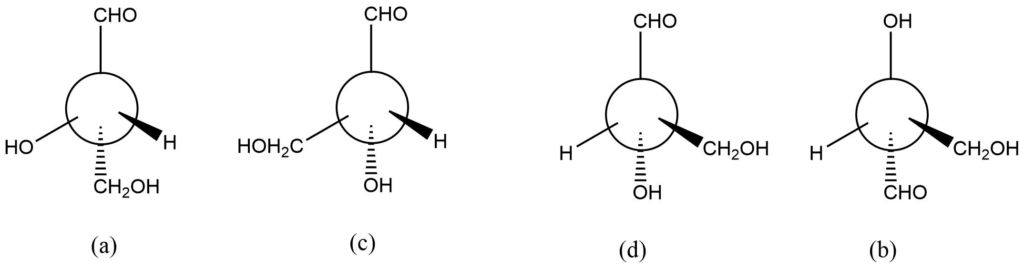
It should be evident that compounds with only one derivative carbon atom can produce only two optically active isomers. As a result, there will only be two distinct molecules (enantiomers) in the figures above, and the two structures produce the same structure.
Each modification in the structure above is produced by transposing a pair of groups. Compound a is transformed into compound c. Compound c changed into compound d, and compound d into compound b. As a result, compound a and c are enantiomers, whereas a and d are identical. Similarly, compounds a and b are enantiomers.
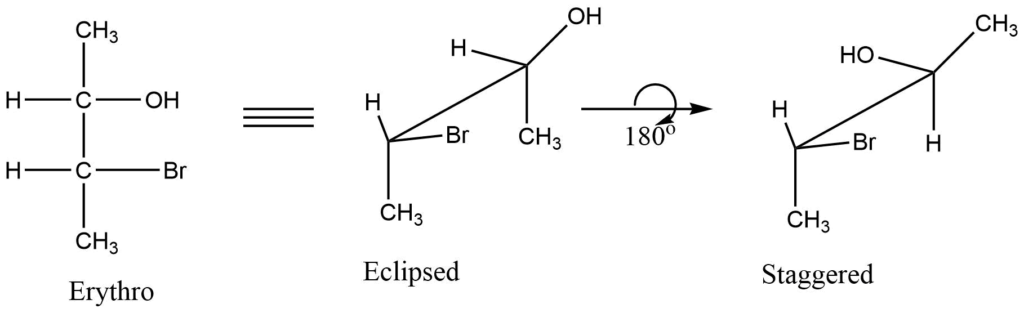
Sawhorse projection of organic compounds
- The sawhorse formula describes how all the atoms or groups in two nearby carbon atoms are arranged.
- Three-dimensional representations of the molecules are displayed.
- Two asymmetric carbon atoms are connected by an oblique line that has been considerably stretched up in length.
- Vertical lines like the Fischer projection formula, represent the groups below the plane of the paper. The erythro and thero isomeric Fischer projection formulas of 3-bromo-2-butanol are shown below in eclipsed and staggered form in the Sawhorse projection formula.
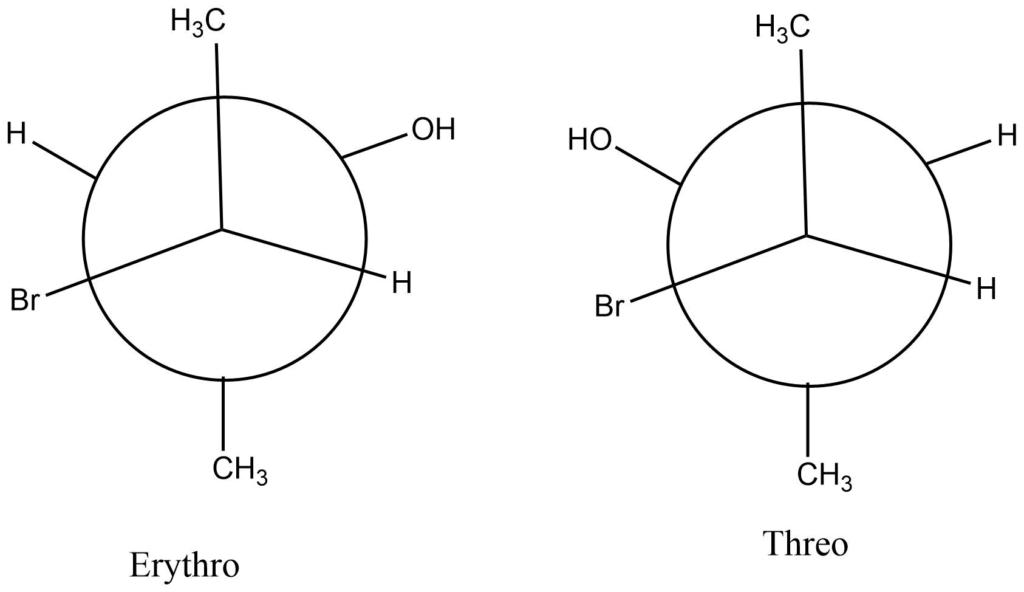
Newman projection of organic compounds
- In these projections, the molecule is viewed from the front or along the axis of a carbon-carbon bond in such a way that the two asymmetric carbon atoms must be one above the other.
- The two asymmetrical carbon atoms are depicted by two superimposed circles. As a result, the formula only contains one circle.
- The circle and bonds linked to asymmetric carbon atoms appear as a wheel and spokes, respectively. The angle between the spokes is 120o.
- Asymmetric carbon bonds at the front of the circle are visible from the center, whereas asymmetric carbon bonds at the back are visible from the circle’s periphery.
for example: 3-bromo2-butanol
The Sawhorse and Newmann projection formulas can be derived from the Newmann projection formula. These equations accurately represent the actual molecular structure of the substances and assess their chemical behavior.
Suggested video
References
- K.R palak,2017, Stereochemistry. Pairavi Prakashan.
- https://byjus.com/chemistry/organic-compounds-structural-formulas/#:~:text=A%20bond%20line%20structural%20formula,methyl%20(%2DCH3)%20group.
- https://www.uou.ac.in/lecturenotes/science/MSCCH-17/CHEMISTRY%20LN%201%20STERIOCHEMISTRY.pdf.
- https://brilliant.org/wiki/structural-representations-of-organic-compounds/
