Radioactivity is the phenomenon of spontaneous disintegration of certain nuclei into other elements with the emission of invisible active radiations. It is a natural phenomenon in which unstable atoms emit radiation to achieve stability.
Interesting Science Videos
Discovery
In 1896 Henri Becquerel discovered radioactivity while investigating the possible relationship between fluorescence and X-ray. A crystal of potassium urinal sulfate was used, a fluorescent material. On exposure to sunlight, it emitted radiations that could penetrate paper glass aluminium sheets. But after a couple of days, Becquerel observed that the uranium salt emitted the same radiations even in darkness. This radiation was named Becquerelrays and the phenomenon of emission of this radiation was named radioactivity.
Soon after this discovery, and after extensive research, Madame Marie Curie and her husband Pierre Curie isolated an element from uranium ore using a laborious method known as chemical fractionating. This new element, which was a million times richer in the mysterious rays than uranium, was given the name radium Madam Curie discovered another radioactive element, polonium, in honor of her native country, Poland.
Nature of radioations
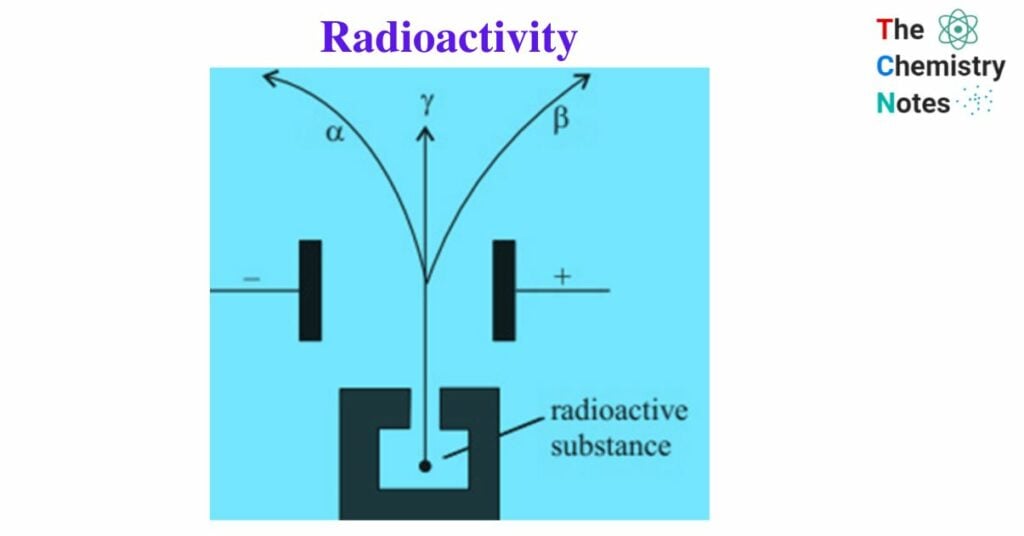
Lord Rutherford, a British physicist, studied the Becquerel rays emitted by radioactive elements in 1899. He demonstrated the existence of two distinct constituents: α- particles and β- rays. P. Villard discovered the existence of γ- rays, the third radiation.
In presence of a magnetic field:
α- particles: are deflected towards the cathode, so they are positively charged.
β- rays: are deflected towards the anode, so they are negatively charged.
Γ- rays: are not affected, hence they are uncharged.
Different characteristics of α-, β-, and γ- rays
| S.N. | Properties | α- rays (or particles) | β- rays (or particles) | γ- rays |
| 1. | Representation | It is represented as 24He or He++. | It is represented as -10e. | It is represented as 00 γ. |
| 2. | The action of the electric field | They deviate towards the cathode. | They deviate towards the anode. | They do not deviate. |
| 3. | Ionizing power | They have high ionizing power, nearly 100 times to that of β- rays. | They have high ionizing power, nearly 100 times that of γ – rays | They have lower ionizing power than α and β-particles. Penetration power |
| 4. | Penetration power | They have little penetration power through solid substances and get scattered by thin foils of metals. They can penetrate a few centimeters of air. | They can penetrate 1-2 m in the air. | They have a greater penetration power than α and β-particles and can penetrate through several centimeters of iron and lead sheets. |
| 5. | Nature of product | The product obtained by the loss of α – particles has an atomic number less by two units and a mass number less by four units than that of the parent element. | The product obtained by the loss of β- particles have an atomic number of more than one unit without any change in mass number. | There is no change in the atomic number as well as in the mass number. |
Characteristic of radioactive rays
- They blacken the photographic plate.
- They pass through thin metal foils.
- They ionize the gas through which they pass.
- They produce luminescence on ZnS, calcium tungstate plate.
- When radioactive rays are passed through an electric or magnetic field it is separated into three component rays namely α-, β-particles and γ-rays.
Nuclear stability
The stability of the nucleus depends on the ratio of the number of neutrons to the protons (i.e., n/p ratio).
When the n/p ratio in the nucleus is equal to one, the most stable nuclei exist for elements up to atomic number 20. Elements with a higher atomic number are more stable if they have a slight excess of neutrons over protons, as this reduces proton repulsion. The n/p ratio exceeds 1.52, from atomic number 84 (PO). The nuclei in these elements increase so large that they become unstable. Nuclear instability occurs when the number of neutrons exceeds the number of protons.
All nuclei with atomic numbers greater than 83 and a mass number greater than 209 are unstable, so they spontaneously transform themselves into lighter ones. Hence, radioactivity is the tendency of the nuclei to readjust the n/p ratio to make a more favorable n/p ratio by emission of α- , β-, and γ- rays to gain stability.
Mass defect and binding energy
According to nuclear particle experiments, the total mass of a nucleus is always less than the sum of masses of its constituent nucleons (i.e., protons and neutrons). Mass defect is the difference between theoretical mass and the actual mass of an atom . It is idenoted by Δm.
Mass defect (Δm) = Theoretical mass – Actual mass (experimental)
= sum of masses of protons and neutrons – Actual mass
The mass difference or mass defect for a nucleus with Z protons and mass number A is ,
Δm= Zmp + (A−Z) mn – mnuc
where Zmp is the total mass of the protons, (A−Z) mn is the total mass of the neutrons, and mnuc is the mass of the nucleus.
The binding energy is the amount of energy released when protons and neutrons (i.e., nucleons) combine to form a nucleus . In other words, the binding energy B of the nucleus is the energy equivalent to mass defect.
B= [Zmp + (A−Z) mn − mnuc] c 2
Protons + Neutrons → Nucleus + Binding energy
Nucleus + Binding energy → Protons + Neutrons
If the mass defect (Δm) is in a.m.u, then binding energy B.E is:
B.E : Δm X 931 MeV ( 1 amu = 931 MeV)
Thus, the higher the mass defect greater will be the binding energy. The binding energy of a nucleus determines its stability against disintegration. If the binding energy is large the nucleus is stable. The binding energy per nucleon is also known as a average binding energy and can be expressed as:
Binding energy per nucleon = Total binding energy/ number of nucleons i.e., mass number
Variation of binding energy per nucleon with mass number
- As the binding energy of nuclei with low mass numbers (e.g., 12H, 13H) is very small, they are unstable. Therefore, such nuclei participate the in the nuclear fusion reaction.
- Nuclei with an equal number of protons and neutrons (e.g., 2He, 12O,) show a rapid increase in their binding energy per nucleon, and hence they are stable.
- The binding energy value reaches its maximum at mass number 56(Fe), indicating the most stable state nucleus.
- As the mass number increase above 80, the binding energy per nucleus decreases resulting in their instability.
Law of radioactive disintegration
Radioactive disintegration is found to obey the following two laws:
- Atoms of all radioactive elements are undergoing spontaneous disintegration with the emission of α-, β- and γ-rays.
- The rate of disintegration is not affected by external factors like temperature, pressure, chemical environment, etc but depends entirely on the law of chance,i.e., the number of atoms breaking per second at any instant is proportional to the number present. In other words, the amount of radioactive element which disintegrates in unit time is directly proportional to the amount of radioactive element present.
Derivation of law of radioactive decay
Suppose a radioactive element A disintegrates into another element B. Let No be the initial amount of A and N be the amount of A left undisintegrated.
A → B
At, t = 0, No
At, t = t, N
As element A undergoes continuous disintegration into B, the number of A goes on decreasing. Hence, the rate of disintegration of A is,
-dN/dt α N
– dN/dt = λ N …………………….(I)
Where λ = decay constant or disintegration constant which is characteristic of each radio element.
The arrangement of equation (I) gives,
dN/N = – λ dt …………………….(II)
Integrating both sides,
∫ dN/N = ∫ – λ dt
In N = – λ t + C……………………………(III)
Where, C = integration constant
Here, When t = 0, N = No
Therefore, In No = – λ x 0 + C
C = In No
Substituting in equation (III) we get,
or, In N = – λ t + In No
or, In N – In No = – λ t
or, In N/No = – λ t……………………….(IV)
or, N/No = e – λ t
N = No e – λ t ………………………….(V)
Thus, the equation may be used to calculate the amount of radioactive element left after a certain time interval. The equation (IV) can be rearranged as:
2.303 log N/No = – λ t
or, 2.303 log No/N = λ t
or, Λ = 2.303/t log No/N ………………..(VI)
t = 2.303/λ log No/N……………….. (VII)
The half-life of radioactive elements
The half-life of a radioactive element is the time required for the disintegration of one-half of the original amount of the radioactive element. The t1/2 value is a measure of the radioactivity of an element. If t1/2 is the half-life period of the radioactive element then at t1/2,
N = ½ No
Substituting the value of No in equation 9V)
No/2 = No e – λ t1/2
or, 1/2 = e – λ t1/2
or, 2 = e λ t1/2
or, In 2 = λ t1/2
or, t1/2 = In2/λ = 0.693/λ ………………..(VIII)
Relation between t and t1/2
we have,
t1/2 = 0.693/λ
λ = 0.693/t1/2
Substituting this value in equation (VII)
t = 2.303/λ log No/ N
t = 2.303/0.693 t1/2 log No/N………………..(IX)
Radioactive series
There are nearly fourteen radioactive elements that occur naturally and are present at the end of the periodic table. When a radioactive element emits α-or β- particles, the new element formed may have an unstable nucleus. In other words, the formation of the stable nucleus from a radioactive element is not one step process. The disintegration process can continue indefinitely until a stable element is obtained. The radioactivity series is the series of elements formed by the successive disintegration of a radioactive element.
The series of elements obtained from 90 232Th, 92 235U, and 92 238U are the natural radioactive series. Hence, there are four series of radioactive elements, which are as follows:
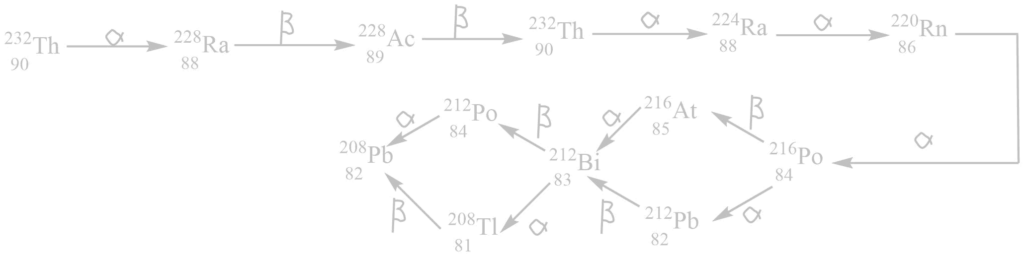
i. Thorium series
It begins with 90232Th and ends with 82208Pb. The mass number of all these elements obtained in this series are integral multiple of 4.
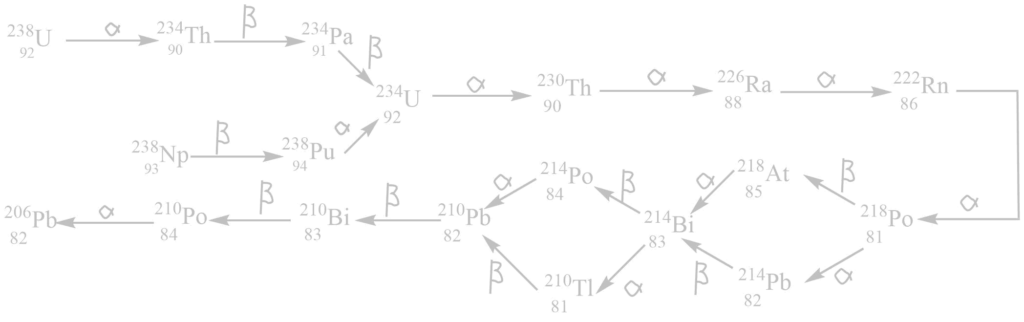
ii. The uranium (4n+2) series
It begins with 92238U and ends with 82206Pb. The mass number of all these elements in this series gives the remainder 2 when divided by 4. Hence, this is called the (4n + 2) series where n is an integer.
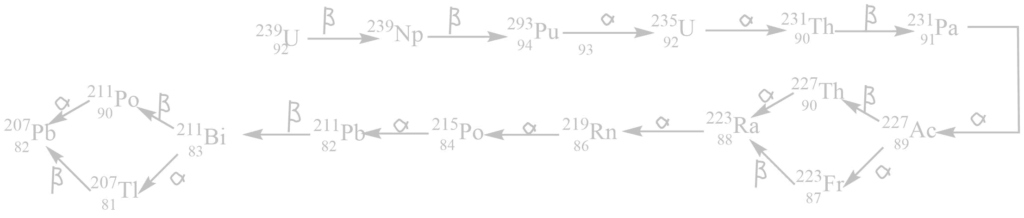
iii. The actinium (4n+3) series
It begins with 92238U and ends with 82206Pb. The mass number of all these elements in this series gives the remainder 3 when divided by 4. Hence, this is called the (4n + 3) series where n is an integer.
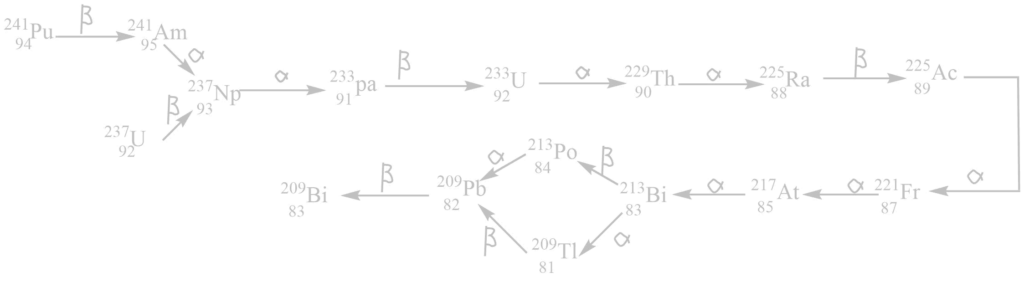
iv. The neptunium (4n+ 1) series
It begins with 94241Pu or 92239U and ends with 83209Bi. The mass number of all these elements in this series gives the remainder 1 when divided by 4. This series is added to the radioactive disintegration series after the discovery of transuranic elements i.e., synthetic radioactive elements. All members of these series are either unknown or very rare in nature.
Recommended video
References
- https://rajdhanicollege.ac.in/admin/ckeditor/ckfinder/userfiles/files/Introduction%20to%20Radioactivity.pdf
- https://www2.lbl.gov/abc/wallchart/teachersguide/pdf/Chap03.pdf
- https://www.britannica.com/science/radioactivity/Occurrence-of-radioactivity
- https://nios.ac.in/media/documents/SrSec312NEW/312_Physics_Eng/312_Physics_Eng_Lesson26.p
- http://www.sfu.ca/~mxchen/phys1021003/P102LN34.pdf
- https://www.nust.na/sites/default/files/documents/Chapter%2012%20%E2%80%93Radioactivity.pdf
- https://byjus.com/physics/radioactivity-alpha-decay/
- https://byjus.com/physics/radioactive-decay/#:~:text=1010%20Bq-,Law%20Of%20Radioactive%20Decay%20Derivation,in%20the%20given%20sample%20material.

