Different atomic orbitals have different shapes. In other words, they describe different probability distributions for the electrons that surround the nucleus. One of the reasons why orbitals vary in energy is because the electrons in various orbitals are likely to be positioned in various locations around the parent nucleus and therefore experience the latter’s attraction with a variety of intensities. It is amazing that despite having different forms, all orbitals in a particular shell of the hydrogen atom have the same energy. This is a result of the elimination of various energy-component contributions.
Interesting Science Videos
Atomic Orbital
Atomic orbitals are mathematical functions that describe how electrons (or electron pairs) behave in an atom.
They provide a method for calculating the likelihood of discovering an electron in a specific area surrounding the atom’s nucleus.
Atomic orbitals have different shapes according to their type. The various atomic orbital shapes indicate which directions have the highest or lowest likelihood of having an electron around the nucleus. The letters s, p, d, and f stand for the four different types of orbitals, each of which has a unique shape.
Shapes of Atomic Orbital
According to the quantum atomic model, an atom can have a very wide range of orbitals. These orbitals fall into category based on their dimensions, shape, or inclination. The possibility of obtaining an electron close to the nucleus rises with a smaller orbital size. The orbital wave function is the mathematical formula for the coordinates of an electron. The square of the orbital wave function represents the likelihood of finding an electron.
The letters s, p, d, and f, which stand for sharp, diffuse, principal, and fundamental, are the symbols for the orbital shapes. The s and p orbitals are the most utilized in organic and biological chemistry, making them the most significant of the four.
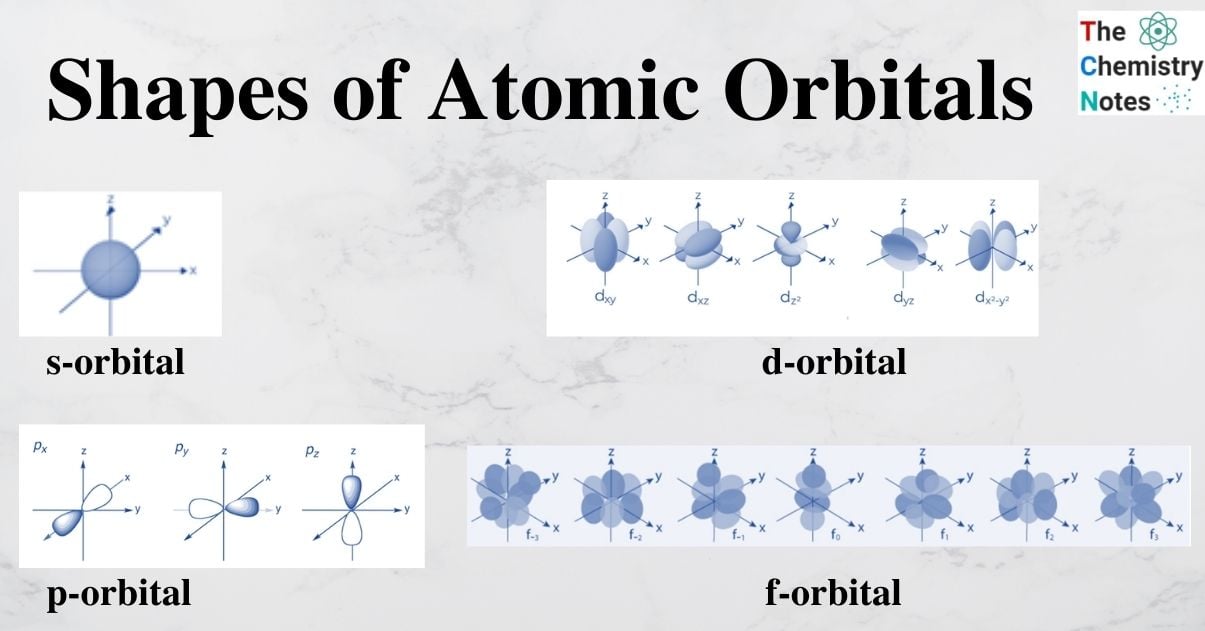
s-orbital
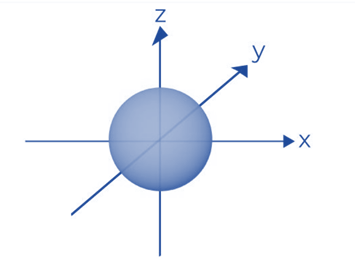
An s orbital has the nucleus of the atom at its center and is spherically symmetric around it, resembling a hollow ball made of relatively fluffy material. The orbitals grow in size as the energy levels rise because the electrons are farther away from the nucleus. The size progression is as follows: 1s, 2s, 3s,…
- The nucleus is at the center of the s orbital boundary surface diagram, which can be represented as a circle in two dimensions.
- Because s-orbitals are spherically symmetric, there is an equal chance of finding an electron in every direction at any given distance.
- It also demonstrates that the size of the s orbital grows as the primary quantum number (n) increases; as a result, 4s > 3s > 2s > 1s.
- A 2s orbital is similar to a 1s orbital, but instead of having one tennis ball inside another, it has an electron density sphere inside the outer sphere. Between the two balls, there is a surface where there is no chance of finding an electron. This surface is referred to as a node or nodal surface. Having three nodes, a 3s orbital is even bigger.
The nodal point is a place where it is impossible to find the electron. There are two categories of nodes: radial nodes and angular nodes. The radial nodes calculate the separation from the nucleus, and the angular nodes calculate the orientation.
p-orbital
s orbitals are only having spherically symmetric orbitals. As the value of l rises, so do the number of orbitals in a given subshell and the complexity of the orbital shapes. There are three 2p orbitals because the 2p subshell has l = 1 and three different values of ml (-1, 0, and +1).
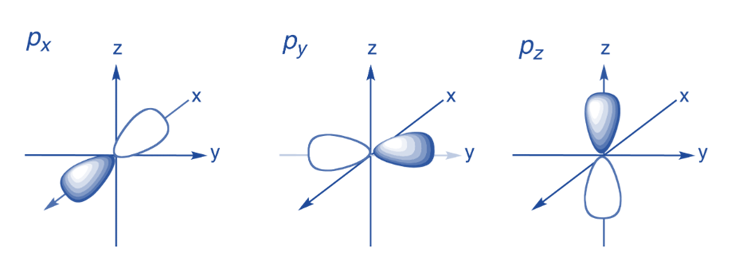
- The p orbitals have a dumbbell-like structure.
- The location of the p orbital node is in the nucleus’s center.
- The p orbital can hold a maximum of six electrons due to the existence of three orbitals.
- The two lobes that make up each p orbital are situated on either side of the plane that crosses the nucleus.
- On either side of the plane that crosses the nucleus, each p orbital has lobes. The probability of finding an electron at the plane where the two lobes intersect is zero.
Because the three orbitals are identical in size, shape, and energy, they are degenerate orbitals. - The position of the lobes is the only distinction between the orbitals. The names 2px, 2py, and 2pz are given to the lobes because they are oriented along the x, y, or z-axis. The number of nodes is determined using the formula n – 2.
- As with s orbitals, p orbitals grow in size and energy as the primary quantum number rises (4p > 3p > 2p).
P orbitals in different shells are different sizes, just like s orbitals. The p orbitals in the shell that are farthest from the nucleus are bigger than those that are closer to the nucleus; for example, a 3p orbital is bigger than a 2p orbital. The size of all p orbitals in a given shell is the same.
d-orbital
According to the axes between or along which their electron clouds are concentrated. There are five d orbitals, with l = 2 and m = -2, -1, 0, +1, and +2. The names of these five d orbitals are dxy, dyz, dx, dx2-y2, and dz2. Among d-orbitals key characteristics are the following:
- Although they have essentially the same energies, the five d orbitals of a given shell have different spatial orientations.
- The only difference between the dxy, dyz, and dxz orbitals is that they are all clover-leaf shapes and their location is in between the axes X and Y, Y and Z, and X and Z, respectively.
- The dx2-y2 orbital is identical to the dxy orbital aside from being rotated by 45 degrees about the Z-axis so that its lobes face the X and Y axes. It also resembles a clover leaf.
- The dz2 orbital is symmetrical about the Z-axis, with the part of the orbital that faces a magnetic field expanding and the part that faces it contracting.
- It is shaped like a dumbbell.
- There are two sets of these five d-orbitals. The angular probability distributions of the dz2 and dx2-y2 orbitals in one set are concentrated along the axial directions, while those of the dxy, dyz, and dxz orbitals are maximum at a 45° angle to the axial directions.
![Shape of atomic orbitals [ Shape of d-orbital]](https://scienceinfo.com/wp-content/uploads/2022/11/image-164.png)
f-orbital
The f- orbital’s shape is extremely intricate. Despite the complexity of the shape, the electron filling rule does not change. The protons align according to the same rules as all other p and d orbitals. Each f orbital is multi-lobed, complex, and has a number of nodal points.
![Shapes of Atomic orbitals [Shape of f-orbital]](https://scienceinfo.com/wp-content/uploads/2022/11/image-165.png)
- The corresponding magnetic quantum numbers for the f orbitals are m1 (-3, -2, -1, 0, 1, 2 3).
- The secondary quantum number for them is I = 3.
References
- Griffiths, David (1995). Introduction to Quantum Mechanics. Prentice Hall. pp. 190–191. ISBN 978-0-13-124405-4.
- Feynman, Richard; Leighton, Robert B.; Sands, Matthew (2006). The Feynman Lectures on Physics – The Definitive Edition, Vol 1 lect 6. Pearson PLC, Addison Wesley.
- https://collegedunia.com/exams/shapes-of-atomic-orbitals-orbitals-chemistry-shapes-of-s-p-d-f-chemistry-articleid-1108
- https://gkscientist.com/shapes-of-atomic-orbitals/
- https://www.sciencefacts.net/atomic-orbital.html
- https://byjus.com/chemistry/shapes-of-orbitals/#:~:text=An%20s%2Dorbital%20is%20spherical,different%20layers%20or%20electron%20shells.
- https://www.expii.com/t/shapes-of-atomic-orbitals-overview-examples-8323
- https://www.geeksforgeeks.org/shapes-of-atomic-orbitals/
- https://www.ck12.org/section/shapes-of-atomic-orbitals/
- https://alevelchemistry.co.uk/notes/atomic-orbital/
- Powell, Richard E. (1968). “The five equivalent d orbitals”. Journal of Chemical Education. 45 (1): 45. Bibcode:1968JChEd..45…45P. doi:10.1021/ed045p45
- Friedman (1964). “The shapes of the f orbitals”. J. Chem. Educ. 41 (7): 354. doi:10.1021/ed041p354
- Atkins, Peter; de Paula, Julio; Friedman, Ronald (2009). Quanta, Matter, and Change: A Molecular Approach to Physical Chemistry. Oxford University Press. p. 106. ISBN 978-0-19-920606-3.
