Thermodynamic processes are the exchanges of energy in the form of heat between or within systems. As we are already well-known for the term thermodynamics. Thermodynamics is the study of energy transfers in a system as represented by the heat, work, and temperature parameters.
A system’s state can change as a result of its interactions with its surroundings. A system’s change can be fast or slow, large or small. A thermodynamic process is a process by which a system’s state can change from an initial to a final state. But before dealing with the further thermodynamic processes let us have some knowledge about quasi-static and non-quasi-static processes.
Interesting Science Videos
Quasi-static and Non-quasi-static Processes
A quasi-static process is one in which the system is in thermodynamic equilibrium with its surroundings at all times. A quasi-static process is a type of thermodynamic process (also known as a quasi-equilibrium process). A thermodynamic process that moves slowly enough to keep the system in internal thermodynamic equilibrium (from the Latin quasi, meaning “as if”). A good example is quasi-static expansion, in which the volume of a system changes so slowly that the pressure remains constant throughout the process.
A quasi-static process is an idealized or imagined process in which the change in state is made infinitesimally slowly so that the system can be assumed to be in thermodynamic equilibrium with itself and the environment at each instant.
Consider heating one kilogram of water from 20oC to 21oC at a constant pressure of one atmosphere. To slowly heat the water, imagine placing the container in a large bath that can be slowly heated so that the temperature of the bath rises infinitesimally slowly from 20oC to 21oC. If we put 1 kg of 20oC water directly into a 21oC bath, the temperature of the water will quickly rise to 21oC in a non-quasi-static way.
All processes in nature are non-quasi-static because quasi-static processes cannot be completely realized for any finite change in the system.
Keep in mind that reversible processes are different from quasi-static ones. A quasi-static process is equivalent to a reversible process when friction is absent.
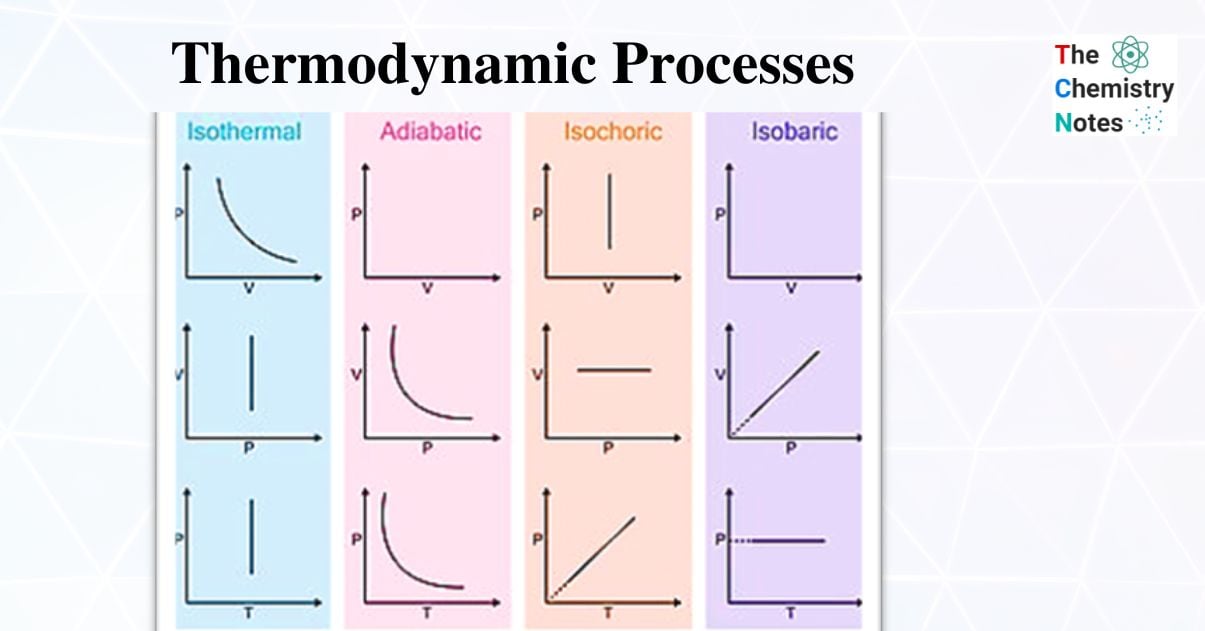
Types of Thermodynamic Processes
Thermodynamic systems can be thought of as enclosed spaces in the universe. Thermodynamic systems are classified into three types: open, closed, and isolated. Different processes can change the state of these systems. Various parameters such as pressure (P), temperature (T), volume (V), and internal energy can be used to express the state of a given thermodynamic system (U). Among different thermodynamic processes we will discuss about four processes in this article and the included topics are:
- Isobaric process in which the pressure (P) is kept constant (ΔP =0).
- Isothermal process in which the temperature (T) is kept constant (ΔT =0).
- Isochoric process in which the volume (V) is kept constant (ΔV =0).
- Adiabatic process in which the heat transfer is zero (Q=0).
- Cyclic Process in which ΔE=0 and ΔH=O.
Let us study in depth about the each processes here;
Isobaric Process
Isobaric is derived from the Greek words isos (constant) and baros (pressure).
Pressure (P) in this process is constant, so the volume of the system changes. Work (W) can be calculated as;
W = P (Vfinal – Vinitial)
Also, W = P * dV
where dV is the change in volume of the system.
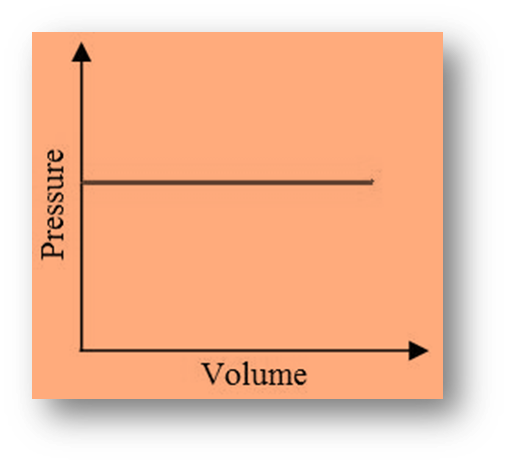
- The work done is positive if V is positive (expansion).
- The work done is negative for negative V (contraction).
For example;
During the boiling of water, the vessel is open. The pressure in the system will not increase or decrease while the vessel is open. It will remain stable. And Isobaric processes are thermodynamic processes in which the pressure remains constant.

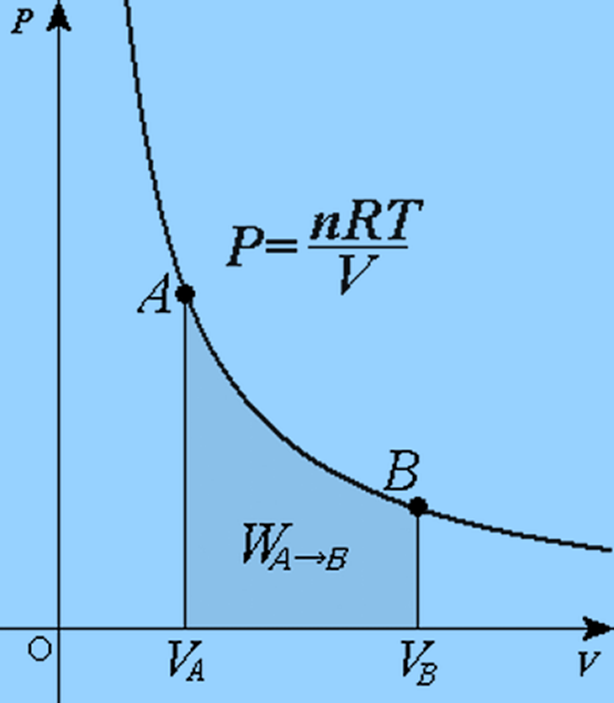
Isothermal Process
The temperature of the system remains constant in an isothermal process.
We know,
W = ∫PdV
From Gas Law,
PV = nRT
P = nRT/V
Using the value of P in the work equation:
W = nRT VB ∫VA (dV/V)
W = nRT ln (VB/VA)
If VB is greater than VA, the work done will be positive; otherwise, it will be negative.
Since internal energy is temperature-dependent, ΔU = 0 because the temperature is constant, and thus,
From the first law of Thermodynamics
(Q = ΔU + W),
we will get Q = W.
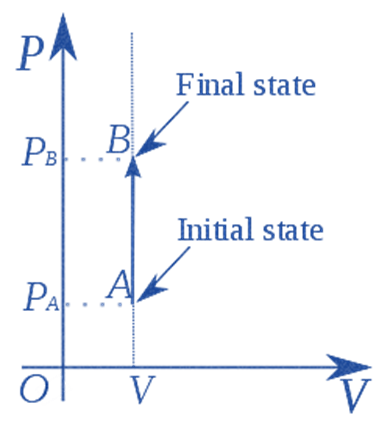
Isochoric Process
In an isochoric process, the volume remains constant. As a result, the system does no work
(Since, V = 0, PV = 0 or W = 0)
A non-changing volume process can be achieved by placing a Thermodynamic system in a closed container that neither contracts nor expands.
As a result of the first law of thermodynamics (Q = U + W), the change in internal energy for an isochoric process becomes equal to the heat transferred (U = Q).
Adiabatic Process
In an adiabatic process (Q = 0), no heat is exchanged with the system.
Its mathematical representation is as follows:
PVꝨ = K (constant)
W also equals PdV. Substituting P for the value in the work equation:
W = ∫PdV
Substituting the value of P in the work equation:
W = K Vf ∫Vi (dV/VꝨ)
W = K [(Vf1-Ꝩ – Vi1-Ꝩ)/ 1-Ꝩ]
Because Q = 0 for an adiabatic process, we can deduce
From the first law of thermodynamics;
(Q = U + W)
So, U = -W
As a result, if the work done is negative, the internal energy will increase, and vice versa.
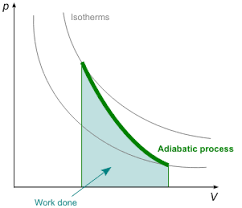
Here is representative image of Adiabatic Process in two states:
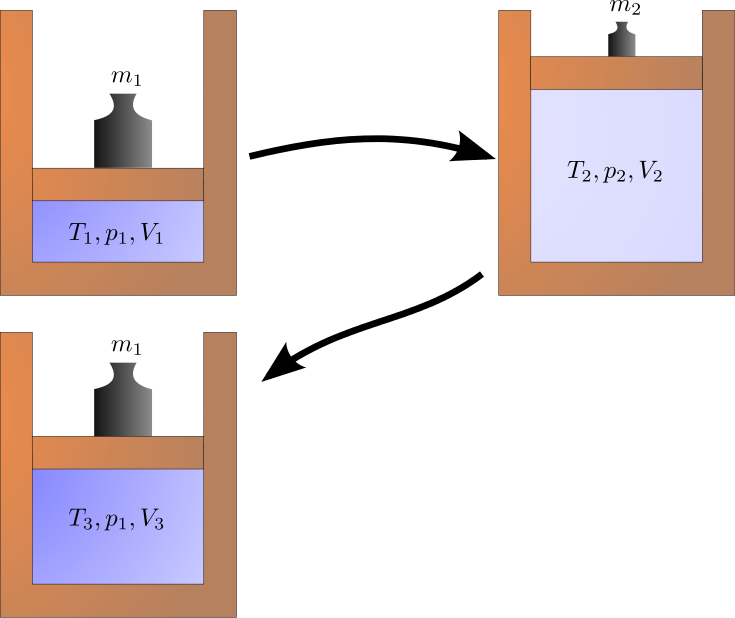

Cyclic Process
A cyclic process is one that eventually returns a system to its initial state. After a cycle, all of the properties have the same value as they did at the start. Because the final state of such a process is the same as the initial state, the total internal energy change must be zero.
ΔU = 0
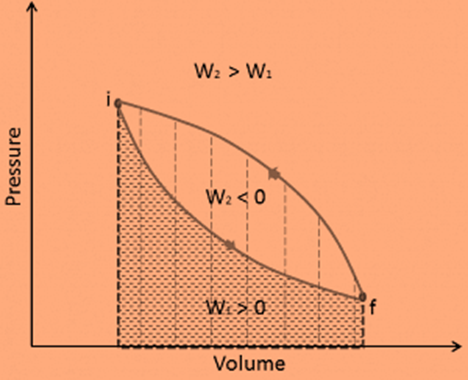
It should be noted that the second law of thermodynamics states that not all heat supplied to a cycle can be converted into an equal amount of work. Some heat rejection is required. The thermal efficiency, ηth, of any heat engine is defined as the ratio of work done, W, to heat input at high temperature, QH.
ηth = W/QH.
Some Other Thermodynamic Processes
Besides these above five thermodynamic processes some other processes are equally important. Other Thermodynamic processes are:
- Reversible Process
- Irreversible Process
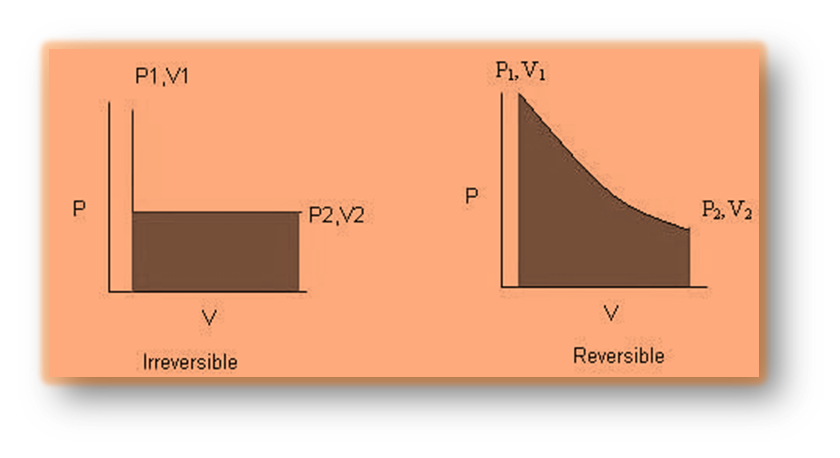
Reversible Process
A reversible process is one that can be reversed, as it can return back to its initial state by very small changes in the system’s properties. There is no increase in the entropy of the system during a reversible process, and the entire system is in perfect equilibrium with its surroundings.
The system’s works in a reversible process,
W = ∫PdV,
where P is the system pressure and V is the volume
Ice cubes can be converted into the water when heated, whereas we get ice cubes when we freeze water. As a result, this is a reversible process.
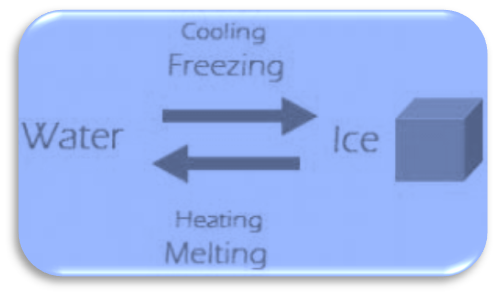
Irreversible Process
The thermodynamics process which cannot be reversed back to its original state is known as irreversible process.
If the entropy of the system increases during a thermodynamic process, the system cannot return to its original state. The surroundings will also undergo thermodynamic changes and will be unable to return to their original or initial state. Hence in this process entropy of the system increases.
References
- Atkins, P.W. and Julio de Paulo, Atkins’ Physical Chemistry, Oxford University Press, UK, Indian Edition 9, 2011.
- R. Chang, “Physical Chemistry for the Chemical and Biological Sciences”, University Science Books, Sausalito, California (2000).
- W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
- U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993
- https://byjus.com/physics/various-processes-in-a-thermodynamic-system/
- https://lawofthermodynamicsinfo.com/thermodynamic-process/
- https://www.toppr.com/guides/physics/thermodynamics/thermodynamic-processes/#Types_of_Thermodynamic_Processes
- https://collegedunia.com/exams/thermodynamic-processes-definition-types-and-solved-examples-physics-articleid-597
