The Van der Waals equation also sometime known as the Van der Waals equation of state. The Van der Waals equation depicts the relationship between real gas pressure, volume, temperature, and quantity. Johannes Van der Waals formulated this equation in 1873. This new equation is an extension of the ideal gas law, which also addresses how molecules in a gas interact and have finite sizes.
Interesting Science Videos
What is Van der Waals Equation?
The Van Der Waals equation describes the relationship that exists between the pressure, volume, temperature, and quantity of actual gases. The real gas equation derivation for a real gas containing ‘n’ moles is as follows.
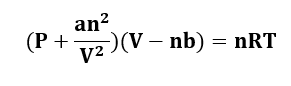
where;
- P stands for pressure.
- V stands for volume.
- T stands for temperature.
- n denotes the number of moles of gas.
- ‘a’ and ‘b’ are van der Waals constants that relate to the intermolecular attractive forces between gas molecules and the volume of the molecules, respectively.
It’s a more advanced version of the ideal gas. This equation, which is made up of non-interacting point particles, obeys the ideal gas law. Gases include certain tiny masses, according to this equation. These masses collide with precision. The actual gas law cannot describe the pattern of real gases. Thus, van der Waal describes the behavior of a real gas as well as the relation between particle surface and number density.
Derivation of Van der Waals Equation
The two postulates utilized in the kinetic theory of gas molecules, according to Van der Waals, do not apply to actual gases. These two assumptions are as follows:
- Gas molecules are either point masses or have no volume.
- In the gas molecules, there is no intermolecular attraction.
The size effect and the intermolecular attraction effect of actual gases were introduced by Van der Waals. These two effects or components in the Van der Waals equation arise from his consideration of gas molecule size and intermolecular attraction. According to van der Waal, in order for the ideal gas equation to be relevant to real gases, the pressure (P) and volume (V) elements in the ideal gas equation must be modified.
Volume correction factor
Real gas molecules are thought to be a hard rigid sphere . As a result, the available space for free movement of molecules is smaller than the initial molar volume.
As a result, the available area for free movement of 1-mole real gas molecules, Vi = V – b,
where
- Vi and V= molar volume of ideal and real gases, respectively. respectively
- b = volume correction factor
The volume correction factor (b) aids in the estimation of the diameter or radius of the gas molecule. As a result of this volume correction method for gases, the ideal gas equation is stated as: Pi (V – b) = RT
Pressure Correction Formula
The gas molecules colliding with the wall creates the pressure of the gas. However, due to intermolecular interaction, the colliding molecules will experience an inward pull. As a result, the pressures exerted by molecules in actual gases will be lower than in ideal gases.
Intermolecular attraction does not exist in ideal gases.
Preal > Pideal
Alternatively, Pideal = Preal + Pa
where Pa denotes the pressure correction term for actual gases
The amplitude of the pressure correction term increases with gas molecule intermolecular attraction. As a result, the pressure correction term is affected by the frequency of molecular collisions. The average pressure exerted by the molecules dropped by Pa, which is proportional to the square of gas molecule density.
As a result, Pa ∝ 1/V2, since density ∝ 1/V
∴ Pa = a/V2
where a denotes the Van der Waals constant for gases
Using the pressure and volume corrections factor formula,
The Van der Waals equation for 1-mole real gas is (P + a/V2)(V – b) = RT.
Since the volume is a significant thermodynamics parameter in this equation, it must vary for n moles of real gases. Thus, for n-mole real gases, the Van der Waals equation of state is
(P + an2/V2)(V − nb) = nRT
Units of Van der Waals constant a and b
The Van der Waals equation is used to calculate the units and dimensions of constants a and b. The Van der Waals equation for n-mole real gases gives
Pa = an2/V2
Pa = unit of internal pressure
Therefore, the unit of Van der Waals constant,
a = atm lit2 mol−2
Again nb = unit of volume, hence unit of Van der Waals constant,
b = lit mol−1
The dimensions of Van der Waals constant,
a = [M L5 T−2 mol−2]
b = [L3 mol−1]
Significance of van der Waals equation
- The equation of Van der Waals may indicate the behavior of a gas more readily and accurately than the equation of ideal gas.
- Van der Waals equations are also employed and are applicable to fluids rather than only gases.
- In terms of volume, the pattern organization of the Van der Waals equation is in the form of a cubic equation.
- The three volumes are given by the equation of cube in volume.
- These three volumes are used to measure the volume at or below the specified critical temperature.
Limitations of Van der Waals Equation
- The equation fails to provide a solution during the gas transition.
- At very high pressures and temperatures, the Van der Waals equation fails.
Signification of volume and pressure correction factor
- The greater the value of the pressure correction factor, the greater the intermolecular attraction and the ease with which the gas may be liquefied.
- The greater the value of b, the bigger the gas molecule. The Van der Waals constant b for carbon dioxide is 0.04 but 0.02 for hydrogen.
Frequently Asked Questions (FAQ)
What is the unit of the Van der Waal constants?
Units of a and b in van der Waals equations are atm litre2 mol–2 and litre mol–1 respectively.
What are the factors that cause gasses to deviate from ideality?
Gases depart from ideality at high pressure and low temperature.
What is the significance of the Van der Waals constants?
The Van der Waal constant ‘a’ represents the magnitude of attraction between gas molecules, whereas the constant ‘b’ represents the effective volume filled by gas molecules.
Video on Van der Waals Equation
References
- https://byjus.com/jee/van-der-waals-equation/
- https://unacademy.com/content/upsc/study-material/chemistry/van-der-waals-equation-of-state-for-real-gases-and-its-derivation/
- https://chemistnotes.com/physical/van-der-waals-equation-units-derivation-and-limitations/
- https://physicscatalyst.com/chemistry/vander-waals-equations.php#google_vignette
- https://collegedunia.com/exams/derivation-of-van-der-waals-equation-real-one-mole-of-gas-physics-articleid-925
- https://testbook.com/physics/derivation-of-van-der-waals-equation
- https://www.priyamstudycentre.com/2019/06/van-der-waals.html

