Young’s modulus is a mechanical property measure for linear elastic solids, such as rods, wires, and the like. It is also known as the elastic modulus or tensile modulus. The elastic properties of a solid undergoing tension or compression in only one direction are described by the numerical constant known as Young’s modulus, which bears the name of the 18th-century English physician and physicist Thomas Young. An example of this would be a metal rod that, when stretched or compressed lengthwise, returns to its original length.

Interesting Science Videos
What is Young’s Modulus?
The Young Modulus of a material is the property that allows it to resist length change due to stress. Another name for Young’s modulus is the modulus of elasticity.
The letters E or Y are used to represent it.
When stress is applied along the x-axis, a solid, such as a rod or wire, will deform along its length. This deformation is measured by Young’s modulus. The deformation of an object in response to applied stress can also be measured using the bulk modulus and shearing modulus.
The relationship between stress (force per unit area) and strain (proportional deformation in an object) is described by Young’s modulus. When a specific load is placed on a solid item, it deforms. If the object is elastic, the body returns to its initial shape when the pressure is released. After a certain degree of deformation, numerous substances lose their linear and elastic properties. Young’s modulus is constant exclusively for linearly elastic materials.
- A solid is elastic if its Young’s modulus is low.
- A solid is considered inelastic or stiff if its Young’s modulus value is high.
Young’s Modulus Formula
Young’s modulus is defined mathematically as the ratio of the strain in the material that corresponds to the applied stress and the stress applied to the material, as follows:
Young’s Modulus = Stress / Strain
Y = σ / ϵ
Where.
Y = Young’s Modulus of the material
σ = stress applied to the material
ϵ = strain corresponding to the applied stress
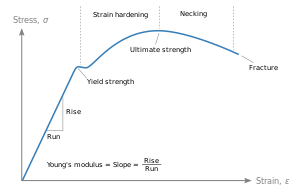
Let us learn a bit about stress and strain as well;
Stress: Stress is the term used to characterize the pushing and pulling forces that cause objects to bend, stretch, or compress. Tensile tension is the term used to describe when something stretches like a rubber band. Compressive stress results from it being squished. Bulk stress occurs when an object is compressed from all sides, for as when it is submerged deeply. Shear stress is the term for the sliding effect that results from sideways-acting forces.
Strain: We refer to this change in size or shape as deformation when it occurs in an item or material under stress. Strain refers to the measurement of this distortion. In tensile stress, bulk stress, or shear stress, strain is given as a fraction that indicates the extent of the change in length, volume, or shape. The number of strain is undefined. This is referred to as tensile strain under tensile stress. Volume strain or bulk strain is what we refer to when the stress is in bulk. Shear strain results from shear stress if that is the reason for the deformation.
Though this relationship isn’t always clear-cut, generally speaking, the more stress you put in, the more strain you get. The linear limit is reached when the stress is sufficiently low for the deformation to be directly proportionate to the stress. The parameter that establishes this linear relationship between stress and strain is known as the elastic modulus. In this linear limit, stress is simply equal to elastic modulus times strain.
Young’s Modulus Factors
A measurement called Young’s modulus can be used to estimate how much a material will bend or deform in response to a given force.
When forced, a material will deform more if its Young’s Modulus is smaller. For instance, the way that clay and wood deform can differ; clay will often deform unevenly, while steel will deform uniformly.
- Deformation may be transient or permanent. Plastic deformation, another name for permanent distortion, persists long after the force is removed. Elastic distortion, also known as temporary deformation, vanishes as the force is released.
- When a material transitions from elastic to plastic deformation depends on its yield strength. Different materials experience plastic deformation in different ways. For example, crystalline solids can slip, but amorphous materials can slide.
- The quality known as plasticity keeps a substance from permanently changing back into its original shape following deformation.
- A material with elasticity can flex under load and revert to its initial shape when the load is released. When stress is released, a fully elastic body returns to its initial state.
- The capacity of a material to stretch into a wire shape when dragged lengthwise under tensile stress is known as ductility.
- The inability of a substance to be stretched into a wire is referred to as brittleness. It deforms very little when it breaks.
How to Calculate Young’s Modulus
This kind of experiment can be used to determine Young’s modulus. One wire for testing and one for reference should be hung from the ceiling. To gauge how much the test wire extends, the reference wire contains a scale. Weights can be added to the test wire to exert various forces.
Here’s what you’ll need to measure:
- The original length of the test wire.
- Calculate the cross-sectional area by measuring the wire’s diameter.
- Measure how much the test wire stretches each time you add weight.
- Plot a graph of stress (force divided by area) against strain (stretch divided by original length).
The slope of this graph gives you Young’s modulus. It’s calculated as the force divided by the cross-sectional area, all divided by how much the wire stretches compared to its original length.
Importance of Young’s Modulus
Young’s Modulus holds a significant place in both industry and academia
- In real-world applications, like construction or manufacturing, knowing Young’s Modulus helps engineers choose the right materials.
- Young’s Modulus is crucial for figuring out how much a material will stretch or deform when a force is applied. Lower modulus values mean the material can stretch more under stress.
- It helps in designing implants and prosthetics that can withstand the stresses inside the body. By understanding how materials behave under stress, medical professionals can create devices that are mechanically suitable for patients.
Modulii of Elasticity
The way a material reacts to stress is measured using its modulus. The stretchiness of a material when pulled along a line is measured by its Young’s modulus. The bulk modulus quantifies the three-dimensional expansion or compression of a material. A material’s shear modulus indicates how much it deforms when twisted or sheared. There are more moduli as well, such as the P-wave and axial moduli. A material’s lateral and lengthwise contractions are compared using Poisson’s ratio. These values explain the behavior of materials under applied forces in conjunction with Hooke’s law.
Young’s Modulus Values
| Material | GPa | Mpsi |
| Aluminum (Al) | 69 | 10 |
| Amino-acid molecular crystals | 21–44 | 3.04–6.38 |
| Aramid | 70.5–112.4 | 10.2–16.3 |
| Bacteriophage capsids | 1–3 | 0.15–0.435 |
| Beryllium (Be) | 287 | 41.6 |
| Brass | 100–125 | 14.5–18.1 |
| Bronze | 96–120 | 13.9–17.4 |
| Carbon fiber-reinforced plastic | 30–50 | 4.35–7.25 |
| Carbon fiber-reinforced plastic | 181 | 26.3 |
| Carbyne (C) | 32100 | 4660 |
| Cobalt-chrome (CoCr) | 220–258 | 29 |
| Copper (Cu) | 117 | 17 |
| Diatom frustules (silicic acid) | 0.35–2.77 | 0.05–0.4 |
| Diamond (C) | 1050–1210 | 152–175 |
| Flax fiber | 58 | 8.41 |
| Glass | 50–90 | 7.25–13.1 |
| Glass-reinforced polyester matrix | 17.2 | 2.49 |
| Graphene (C) | 1050 | 152 |
| HDPE | 0.8 | 0.116 |
| Hemp fiber | 35 | 5.08 |
| High-strength concrete | 30 | 4.35 |
| Human Cortical Bone | 14 | 2.03 |
| Low-density polyethylene | 0.11–0.86 | 1.6–6.5×10−2 |
| Magnesium (Mg) | 45 | 6.53 |
| Medium-density fiberboard (MDF) | 4 | 0.58 |
| Molybdenum (Mo) | 329–330 | 47.7–47.9 |
| Mother-of-pearl nacre (calcium carbonate) | 70 | 10.2 |
| Nylon | 2–4 | 0.29–0.58 |
| Osmium (Os) | 525–562 | 76.1–81.5 |
| PTFE (Teflon) | 0.5 | 0.075 |
| Polycarbonate | 2–2.4 | 0.29-0.36 |
| Polyethylene terephthalate (PET) | 2–2.7 | 0.29–0.39 |
| Polypropylene | 1.5–2 | 0.22–0.29 |
| Polystyrene, foam | 2.5–7×10-3 | 3.6–10.2×10-4 |
| Polystyrene, solid | 3–3.5 | 0.44–0.51 |
| Rubber (small strain) | 0.01–0.1 | 1.45–14.5×10−3 |
| Silicon carbide (SiC) | 450 | 65 |
| Silicon crystal | 130–185 | 18.9–26.8 |
| Single-walled carbon nanotube | 1,000+ | 150+ |
| Steel (ASTM-A36) | 200 | 29 |
| Stinging nettle fiber | 87 | 12.6 |
| Tooth enamel (calcium phosphate) | 83 | 12 |
| Titanium (Ti) | 110.3 | 16 |
| Titanium alloys | 105–120 | 15–17.5 |
| Tungsten (W) | 400–410 | 58–59 |
| Tungsten carbide (WC) | 450–650 | 65–94 |
| Wood (along grain) | 11 | 1.60 |
| Wrought iron | 190–210 | 27.6–30.5 |
| Yttrium iron garnet (YIG) | 193-200 | 28-29 |
References
- https://unacademy.com/content/cbse-class-11/study-material/physics/youngs-modulus/
- https://alevelphysics.co.uk/notes/youngs-modulus/
- https://www.toppr.com/guides/physics-formulas/youngs-modulus-formula/
- https://www.britannica.com/science/Youngs-modulus
- https://byjus.com/physics/youngs-modulus-elastic-modulus/
- Helmenstine, Anne Marie, Ph.D. “What Is Young’s Modulus?” ThoughtCo, Feb. 17, 2021, thoughtco.com/youngs-modulus-4176297.
- https://www.geeksforgeeks.org/youngs-modulus/
