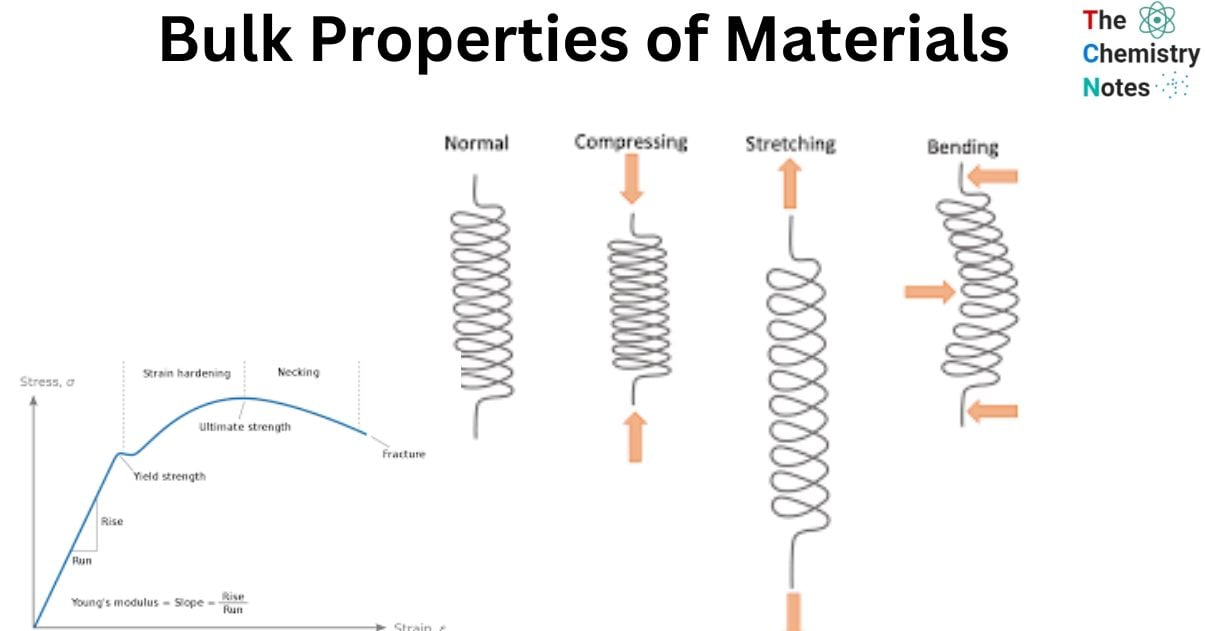
Bulk properties refer to the mechanical properties that emerge from the collective behavior of atoms or molecules subsequent to their bonding. Several significant bulk properties comprise elasticity, tensile strength, density, hardness, electrical conductivity, and thermal conductivity.
Atoms, on their own, do not possess the same physical characteristics as the substances in which they are found. For instance, a single atom of copper is unable to carry electricity, despite the fact that copper itself is capable of doing so. Bulk qualities are those that arise from a large number of atoms, ions, or molecules interacting with one another.
Carbon atoms have a complete outer shell of four electrons, which allows them to form chemical bonds with other elements. When carbon atoms come together to form a diamond, they share the electrons that are created as a result of this bonding process. The atoms of carbon are forced together to create a solid crystal structure when the environment is extremely hot and pressurized. As a result of its structure, the diamond is extremely tough, and because it does not contain any free electrons, it does not react with acids.
Hardness, electrical conductivity, thermal conductivity, elasticity, density, and tensile strength are all essential qualities of solids. Other important properties include tensile strength and density.
Interesting Science Videos
Bulk Properties of Matter In Mechanics
The macroscopic characteristics of materials can provide valuable insights into their response to mechanical stimuli such as stress and pressure. The mechanical properties of hardness and elasticity are of great importance and should be duly considered. It is imperative to possess a comprehension of the manner in which discrete forces and weights will influence the response of materials.
- Flexibility is a crucial requirement for specific materials, such as eyeglass frames, to prevent fracture under compressive forces. Furthermore, it is imperative to consider other fundamental characteristics such as tensile strength, bulk modulus, and density.
- The aforementioned attributes are, to a certain degree, regulated by the chemical bonds that are present among the particles. Ceramics exhibit ionic bonding, whereas polymers are characterized by covalent bonding and metals display metallic bonding. The bonding interactions not only exert an influence on the mechanical characteristics of the material, but also on its structural attributes.
- Bonds can be conceptualized as springs that establish a connection between atoms. The strength of metallic bonds surpasses that of the bonds observed in a rubber band.
![Elasticity of rubber [Bulk properties of solid]](https://scienceinfo.com/wp-content/uploads/2023/06/image-230.png)
An analogy of springs could be used to illustrate how a material’s constituent parts relate to the property of elasticity of the substance. Each material has springs that have varying degrees of stiffness.
- The rubber band molecule is composed of lengthy chains that are intertwined with one another. They undergo an arrangement change as a result of being tugged by a force, which causes them to become more elongated.
- When a rubber band is stretched, its molecules within the band become less entangled, which enables the band to grow in size.
- The key difference between a rubber band and a diamond or a metal is that both of those items possess a compact, linearly compressed structure that prevents them from elongating to a significant degree.
Additionally, other bulk properties, like as the melting temperature, are susceptible to being influenced by the type of connection. Materials that have ionic, covalent, or metallic bonds have melting values that are higher than those containing hydrogen bonds, such as van der Waals’, which have lower melting points. Bulk properties of materials are discussed below:
Elasticity
The ability of a substance to stretch in response to the impact of an external force and then revert to its initial form when that force is released is referred to as its elasticity.
- In the fields of science and manufacturing, where specific kinds of labor and tasks require elastic materials, elasticity is a feature that is considered to be very significant.
- During the event of a car collision, for instance, the components that make airbags have to be able to endure severe forces and rapidly changing shapes whilst yet maintaining their integrity.
- Pascals are used as the standard unit of measurement for elasticity. A mechanical test must be conducted to carry out the calculation. This test is often performed by stretching a material while applying a force denoted by using the symbol ‘F,’ as demonstrated in the diagram that follows.
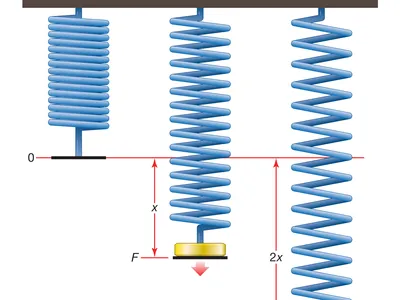
The mechanical stress causes the material to shorten or lengthen as a result. After that, it reverts back to its initial length provided that it has not reached its ‘elastic limit’ yet.
The ability of a material to withstand forces without experiencing permanent deformation is directly linked to its elasticity. Young’s modulus, which is expressed in Pascals, is a property that is essential to elastic materials and is named after its namesake.
Young’s Modulus
- The proportion that exists between the strain (deformation) that material experiences and the mechanical stress that it is subjected to is what is known as the Young modulus.
- In a tensile test, the amount of material that is deformed, measured as strain, is proportional to the amount of force that is applied, measured as mechanical stress. The slope that is produced is proportional to Young’s modulus.
- After being deformed, the material will return back to its initial shape in the section of the space that has been designated as the “elastic zone.” The elasticity modulus, commonly referred to as Young’s modulus, can be calculated by determining the slope of the red line. This varies depending on the type of material being used, as the table that follows demonstrates.
| Materials | Young’s Modulus (GPa) |
|---|---|
| Polystyrene | 3 – 3.5 |
| Aluminium | 68 |
| Glass | 50 – 90 |
| Copper | 117 |
| Diamond | 1210 |
To derive the Young modulus from a plot of stress vs strain, we must first determine what is the slope of the trajectory while it is in the area of elasticity. If you’re familiar with two points on the stress vs. strain curve, then you can accomplish this quickly by utilizing the formula that is provided below.
Modulus = (y2-y1)/(x2-x1)
= (σ2-σ1)/(ε2-ε1)
= Δσ/Δε
The tensile stress is referred to as the amount of force that is employed for deforming the material separated by the cross-sectional region of the material, whereas the tensile strain ε is specified as the rise in length divided by the initial length of the material. This is reflected in the formulas that are provided below.
σ = F / A
ε = δI / I
Hooke’s Law
Hooke’s law can be used to simulate the region of a material that is responsible for its elastic behavior. In this particular situation, an analogy is very helpful. The weight of the force that is being exerted on the material can be interpreted as equivalent to the pull of gravity, and the elasticity of the material can be regarded as a spring which is being compressed by the force.
In this particular instance, the force exerted is directly proportional to the elongation as well as the spring constant k.
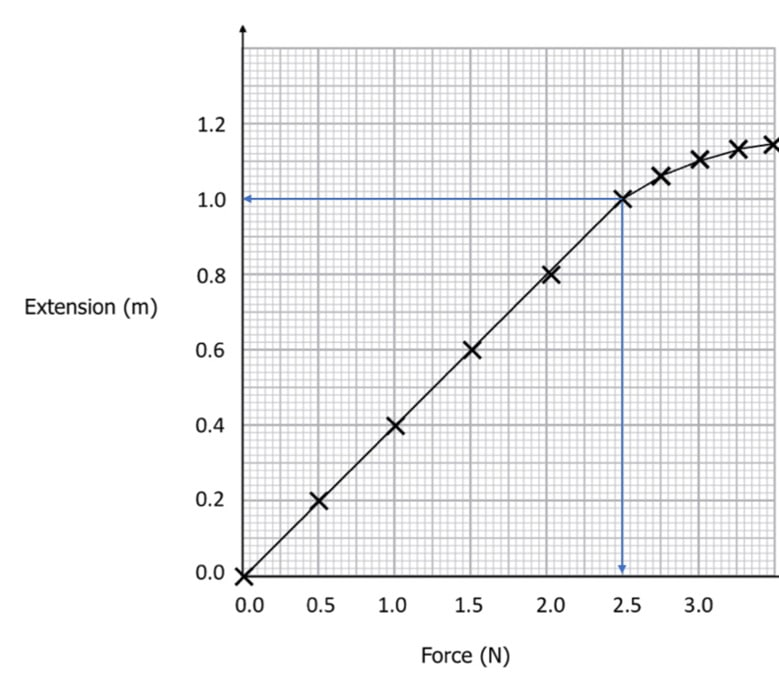
Plasticity
When materials are stretched beyond their elastic limit, they enter what is known as the plastic zone, which is the point at which they begin to irreversibly deform as the force continues to pull them. The disruption of the linear relationship that exists between tensile stress and tensile strain marks the beginning of the plastic zone in a material.
Hardness
It is referred to as a substance’s hardness when it can resist being scraped or penetrated, and its hardness is measured in Pascals.
In many instances, the elasticity of a material has a relationship with its degree of rigidity. Because the atoms and molecules in the material’s structure make it feasible for the substance to elongate, a force applied to a fragment of the material’s surface can penetrate it. This is because, due to the molecules and atoms in the material, the impact can penetrate. Because the strength of their linkages and structures prevents a force attempting to push them from piercing them, materials like metals and diamonds lack elasticity. This is in contrast to materials that have high elasticity and can spring back after being stretched.
Density
The concept of density is characterized by the ratio of the mass of a substance to its volume. It is imperative to adhere to standard units when computing density. Hence, it is typical to observe density being denoted in units of kgm-3. Alternative units for density, such as gm-3 or gcm-3, may also be observed.
Density is calculate using:
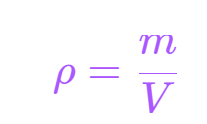
- ρ is the density in kilograms per metres cubed(kgm−3)
- m is the mass in kilograms (kg)
- V is the volume in metres cubed (m3)
A substance exhibiting high density is characterized by a significant quantity of mass that is densely packed within a restricted volume, as exemplified by a lead cube or brick.
A substance exhibiting reduced density possesses a lesser quantity of mass in relation to its volume, as exemplified by objects like sponges or air-filled balloons.
References
- https://www.physicsandmathstutor.com/physics-revision/a-level-aqa/mechanics-and-materials/
- https://www.bbc.co.uk/bitesize/guides/z3ntjty/revision/4
- https://mmerevise.co.uk/a-level-physics-revision/bulk-properties-of-solids/
- https://slideplayer.com/slide/13485166/
- https://shiken.ai/physics/bulk-properties-of-solids
- https://www.britannica.com/science/elasticity-physics
- https://www.studysmarter.co.uk/explanations/physics/mechanics-and-materials/bulk-properties-of-solids/
