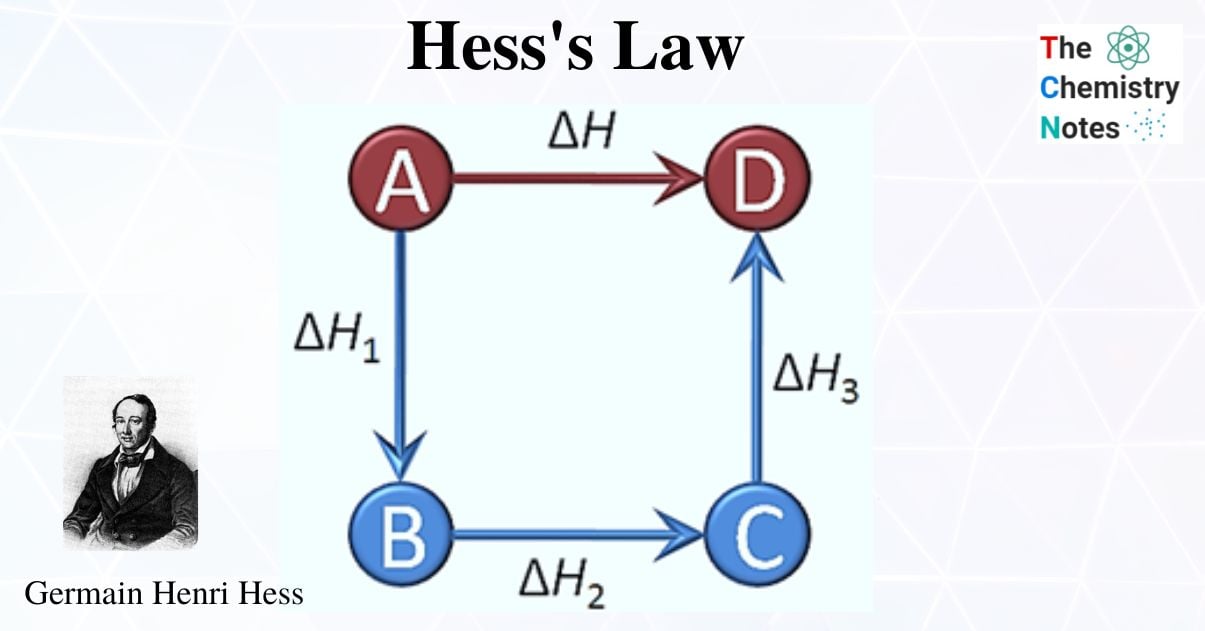
Directly determining the enthalpy change for a chemical reaction can be challenging in some cases. It might be challenging to manage the reaction that is occurring in a lab. Alternatively, taking measurements from the reaction mixture using conventional calorimetry techniques may be difficult. The enthalpy change for the reaction is the same whether it occurs in one step or a series of multiple steps because we know that enthalpy is a state function and that it is independent of the path between the initial state and the final state. This is explained in the form of Hess Law.
Interesting Science Videos
Hess’s Law of Constant Heat Summation– Statement
Additionally known as the Hess law of constant heat summation, is one of the key consequences of the first law of thermodynamics. Whether a chemical or physical process is carried out in one step or several steps, the enthalpy change is the same in both cases.
Hess’s Law states,” The heat evolved or absorbed in a given chemical reaction is always the same, regardless of whether the process takes place in a single step or a series of steps.”
In 1840, Germain Hess, a Swiss-born Russian chemist and physician, derived Hess’s law of constant heat summation from a thermochemistry relationship for calculating the standard reaction enthalpy for the multi-step reactions. In general, it renders use of the properties of state functions, where the value of the state function is independent of the path taken for dissociation or formation. Instead, it only depends on the current state.
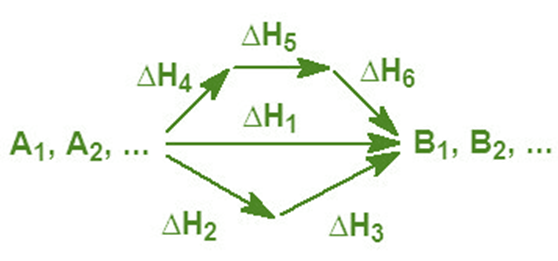
The particular route that leads to the formation of the various B products from the A reactants has no direct effect on the overall enthalpy change. ΔH1 = ΔH2 + ΔH3 = ΔH4 + ΔH5 + ΔH6.
Hess’s Law Equation
Let us suppose that substances A to change Z as;
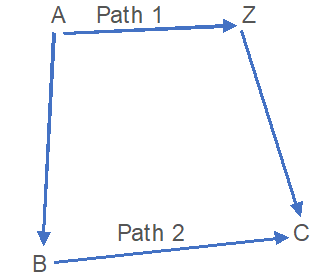
- In single step:
A → Z [Q1 = HZ– HA]
- By Multiple steps:
a) A → B [q1 = HB-HA]
b) B → C [q2 = HC-HB]
c) C → Z [q3 = HZ-HC]
Now, the total heat evolved in these steps;
Q2 = q1 +q2 + q3
∴ Q2 = Q1
Theoretical Justification of Hess’s Law Equation
If Q1 > Q2, then in one cycle ( Q1 – Q2) amount of heat is created. By repeating the cycle, unlimited heat can be created, but this discards the first law of thermodynamics. So, to obey the first law of thermodynamic, Q1 must be equal to Q2.
Illustration of the Hess Law
Let us consider a example of formation of CO and CO2.
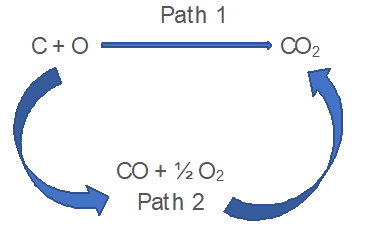
- In Path 1; The enthalpy change is -393.5kJ
C (s) + O2 (g) ⟶ CO2 (g); ΔH = -393.5kJ
- In Path 2;
C (s) + 1/2 O2 (g) ⟶ CO (g); ΔH1 = -110.5kJ
CO (g) + 1/2 O2 (g) ⟶ CO2 (g); ΔH2 = -283.0kJ
C (s) + O2 (g) ⟶ CO2 (g); ΔH = -393.5kJ
∴ ΔH = ΔH1 + ΔH2
Application of Hess’s Law
In addition to calculating the enthalpy of a reaction rather than directly measuring it. Hess’s law uses:
- Determine electron affinities using theoretical lattice energy.
- Determine the heat change of phase transitions.
- In a reaction, calculate the heat of formation of an unstable intermediate.
- Determine the ionic compound’s lattice energy.
- Calculate the heat change that occurs when a substance changes allotropes.
Allotropes of carbon include carbon and diamond. However, because these processes cannot be carried out spontaneously, it is impossible to measure the energy change in the transformation of graphite into diamond. Nonetheless, the heat changes for this hypothetical physical change are calculated using Hess law.
The heat of reaction for graphite and diamond with oxygen is -393.4kJ and -395.4kJ, respectively.
C (graphite) + O2 ⟶ CO2 (ΔHg) = -393.4kJ
C (diamond) + O2 ⟶ CO2 (ΔHd) = -395.4kJ
C (graphite) + O2 ⟶ CO2 (ΔHd) = -395.4kJ
Reversing the diamond combustion reaction:
CO2 ⟶ C (diamond) + O2 (ΔHd) = + 395.4kJ
Putting it all together,
C (graphite) + O2 ⟶ CO2 (ΔHg) = – 393.4kJ
C (graphite) ⟶ C (diamond) (ΔH)= +2.0kJ
Endothermic 2KJ enthalpy change occurs in the allotrope transition of graphite to diamond.
Importance of Hess’s Law
There is energy inside every substance (atom, molecule) which depend upon its temperature, internal force, and nature of the force existing. Some bonds connecting atoms are broken and new bonds are formed when the substance undergoes chemical reactions and these processes require energy. Hess’s law is valid, so it is possible to divide a chemical reaction into different steps and calculate the total energy of the reaction using the standard enthalpies of formation. Empirical data, typically obtained through calorimetry, are used to create standard enthalpy tables. Therefore, it is possible to determine whether or not a more complicated reaction is thermodynamically favorable using these tables.
For instance, carbon and excess oxygen can react to form carbon dioxide. Directly or indirectly, when carbon and oxygen combine, carbon dioxide is produced, either first as carbon monoxide and then as carbon dioxide. Only the energy changes associated with the formation of carbon dioxide will be revealed by measurement; not for carbon monoxide.
Similar to this, it is impossible to determine the enthalpy of benzene formation from carbon and hydrogen because under the conditions present, carbon and hydrogen may also combine to form other types of hydrocarbons in addition to benzene.
The only method for calculating such immeasurable enthalpy changes in physical and chemical changes is Hess’s law. Hence, this is the most important significance of this law.
Steps for Solving Hess’s Law questions
- Find a reaction step in the overall reaction that includes each reactant and product. A single process may involve several reactants or products. However, you might need to come up with a response for each.
- Reverse any necessary reactions if necessary. Most importantly, don’t forget to update the enthalpy’s sign.
- By multiplying, you can change the mole ratios. Hence, do not forget to multiply the enthalpy as well.
- To create the overall reaction, add the step reaction. Cancel anything that is on a product and reactants.
- Finally, add the step reactions’ enthalpies changes. You currently have the overall reaction’s enthalpy change.
Illustration
Calculate the enthalpy for NO (g) + O (g) → NO2 (g).
Given:
- NO (g)+O3 (g) → NO2 (g) + O2 (g); ΔH=−199.0KJ
- O3 (g) → 32O2 (g); ΔH=−142.0KJ
- O2(g) → 2O (g); ΔH=495.0KJ
Step 1: It is clear that both nitrogen dioxide and oxide are present in the first equation. But it also contains diatomic oxygen and ozone. Hence, to eliminate them, we must use the other equations.
Step 2: We must reverse the third equation because to be a reactant, we need singlet oxygen, We must also reverse the second equation We must remove ozone from the first equation.
- NO (g) + O3 (g) → NO2 (g) + O2 (g); ΔH=−199.0KJ
- 32O2 (g) → O3 (g); ΔH=+142.0KJ
- 2O (g) → O2 (g); ΔH=−495.0KJ
Step 3: We now divide the third equation in half. because the reactant only requires a single singlet oxygen.
1/2 [(2O (g) → O2 (g)]; 1/2 (ΔH=−495.0KJ)
O (g) →1/2 O2 (g); ( ΔH=−247.5KJ)
Step 4: Additionally, we can add the three equations.
NO (g) + O3 (g) → NO2 (g) + O2 (g)
32O2 (g) → O3 (g)
O (g) → 12O2 (g)
Overall: NO (g) + O3 (g) + 32O2 (g) + O (g) → NO2 (g) + O2 (g) + O3 (g) + 12O2 (g)
Step 5: Finally, we add the enthalpies.
ΔH=−199.0KJ + 142KJ+ (−247.5KJ) =−304.5KJ.
Reference
- Atkins, P.W. and Julio de Paulo, Atkins’ Physical Chemistry, Oxford University Press, UK, Indian Edition 9, 2011.
- R. Chang, “Physical Chemistry for the Chemical and Biological Sciences”, University Science Books, Sausalito, California (2000).
- W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
- https://www.vedantu.com/chemistry/hesss-law
- https://byjus.com/jee/hess-law-of-constant-heat-summation/
- https://thefactfactor.com/facts/pure_science/chemistry/physical-chemistry/hesss-law-and-its-applications/6881/
- https://www.expii.com/t/hesss-law-of-heat-summation-overview-examples-8693
- https://collegedunia.com/exams/hess-law-applications-calculation-process-use-chemistry-articleid-598
