
Quantum numbers are used to completely explain the movement and trajectories of each electron within an atom. There are four different quantum numbers. The combination of all quantum numbers of all electrons in an atom is characterized by a wave function that obeys the Schrödinger equation.
The study of quantum mechanics and the spectrum revealed that an electron in an atom displayed four states. These four states are (i) shell, (ii) sub-shell, (iii) orbital, and (iv) electron spin direction. To specify these four states of an electron it requires a set of four numbers called quantum numbers. These four quantum numbers are-
(1) Principal quantum number: (n)
(ii) Azimuthal or subsidiary or angular momentum quantum number (I).
(iii) Magnetic quantum number (ml or m)
iv) Spin quantum number: (ms or s)
so, quantum numbers are a set of numbers used to characterize the position and energy of an electron in an atom.
When Schrodiltcer wave equations obtain physically relevant values for Ψ, these quantum numbers emerge naturally as constants. The spin quantum number cannot be calculated using the Schrodinger wave equation. It is acquired either through spectroscopic measurements that account for electron spin (Ulhenbeck and Goudsmith) or through a quantum mechanical treatment of Dirac that includes relativistic effects.
These quantum numbers describe an electron’s energy and position. When these four quantum numbers are combined, they provide a comprehensive representation of an electron in an atom. Each electron in an atom has a distinct set of quantum numbers; according to the Pauli Exclusion Principle, no two electrons may have the same four-quantum-number combination. Quantum numbers are also utilized for analyzing atomic properties such as ionization energy and atomic radius.
These four quantum numbers are described below.
Interesting Science Videos
Principal quantum number
The principal quantum number is denoted by the symbol n and can have values 1, 2, 3, and 4, It can take all non-zero positive integral values from 1 to ∞. i.e.,
n = 1, 2, 3, 4, 5,……. ∞.
It provides the energy of an electron as well as the size of the orbital (the distance from the nucleus to the orbital).
The label “principal” is assigned because appropriate values of other quantum numbers i.e., l and m can only be specified after determining an acceptable value of n. The fundamental quantum number is independent. Bohr proposed it to account for the restricted character of an atom’s energy level as well as the line spectrum of hydrogen. The following are some of the most important implications of the primary quantum number.
Significance of principal quantum number
I. It gives the average distance of the electron from the nucleus. It is given by,
r = n2 x 0.529 x 10-10 m
As it describes the most probable distance between the nucleus and the electrons, a higher value of the primary quantum number signifies a greater distance between the electron and the nucleus.
II. It gives the maximum number of electrons that can accommodate in the shell.
All orbitals with the same n value are considered to belong to the same shell (level). For a given n integer, the total number of orbitals for a given n value is n 2. The total number of electrons for a given n value is 2n 2.
| Shell | n | Maximum electrons (2n2) |
| K | 1 | 2 X 12 = 2 |
| L | 2 | 2 X 22 = 8 |
| M | 3 | 2 X 32 = 18 |
| N | 4 | 2 X 42 = 32 |
| O | 5 | 2 X 52 = 50, and so on |
III. The energy of an electron in hydrogen-like systems
The principal quantum number gives the energy of the electron in all hydrogen and hydrogen-like species by the following relation.
E = -1312/ n2 kJ/ mol
i.e., the energy of the electron increases as the value of n increase and become zero at infinity.
Azimuthal quantum number
The azimuthal quantum number is represented by the symbol I and can have values of n—l, n—2, n—3,….0. The azimuthal quantum number is also known as the “angular momentum quantum number” because the values of l govern the orbital angular momentum of the electron in a given quantum mechanical state.
Somnterfeld proposed the azimuthal quantum number to explain the development of fine structures in hydrogen. The orbital angular momentum quantum number is determined by this quantum number. It is written as,
mvr = √l(l+1) h/2∏
where, l = Azimuthal quantum number)
The energy of electrons is divided not merely into principal energy levels denoted by n but also into sub-energy levels denoted by l. It signifies that the shells are divided into sub-shells. A second quantum number, known as the azimuthal quantum number, is utilized to specify these sub-shells. It is represented by the letter ‘l’. It can have any positive integer value between 0 and (n-1).
The azimuthal (or orbital angular momentum) quantum number characterizes the shape of an orbital. Its value is equal to the orbital’s total number of angular nodes. A value of the azimuthal quantum number can represent an s, p, d, or f subshell of varying shape. This value of the azimuthal quantum number depends on the value of the principal quantum number, i.e. the value of the azimuthal quantum number ranges between 0 and (n-1).
Significance of azimuthal quantum number
The value of the azimuthal quantum number(l) determines the following properties associated with electrons.
I. It gives the number of subshells present in the given shell.
For K shell (First shell)
n = 1
l = 0 (s sub-shell)
There is only one value of ‘l ‘ for the K shell. It represents that K shell has only one sub-
shell and designated as Is. (l = O)
For L shell (Second shell)
n = 2
l = 0 and 1 (p sub-shell)
There are two values of I for the L shell. It represents that it has two sub-shells and
designated as 2s (l = 0) and 2p (l = 1)
For the M shell (Third shell)
n = 3
l = 0, 1, and 2 (d sub-shell)
Three values of I for M shell represent that it has three sub-shell and is designated as
3s (l = 0), (l = 1) and 3d (l = 2).
For N shell (Fourth shell)
n = 4
l = 0, 1, 2, and 3 (f sub-shell)
Four values of l for n shell represent that it has four subshells and is designated as 4s (l=0), 4p (l=1), 4d (1=2), and 4 f (l=3).
For example, if n = 3, the azimuthal quantum number can be 0, 1, or 2. When l is set to zero, the resulting subshell is an’s’ subshell. Similarly, for l=1 and l=2, the resulting subshells are ‘p’ and ‘d’ subshells. As a result, for n=3, the available subshells are 3s, 3p, and 3d.
Summary table
| l = 0 | l = 1 | l = 2 | l = 3 | l = 4 | l = 5 | |
| n = 1 | 1s | |||||
| n = 2 | 2s | 2p | ||||
| n = 3 | 3s | 3p | 3d | |||
| n = 4 | 4s | 4p | 4d | 4f | ||
| n = 5 | 5s | 5p | 5d | 5f | 5g | |
| n = 6 | 6s | 6p | 6d | 6f | 6g | 6h |
| n = 7 | 7s | 7p | 7d | 7f | 7g | 7h… |
| n = 8 | 8s | 8p | 8d | 8f | 8g | 8h… |
II. It gives a maximum number of electrons that can accommodate in the sub-shell.
This can be given by ( 4l +2)
| Subshell | l | Maximum electron (4l+2) |
| s | 0 | 4 x 0 +2 = 2 |
| p | 1 | 4 x 1 +2 = 6 |
| d | 2 | 4 x 2 +2 = 10 |
| f | 3 | 4 x 3 +2 = 14 |
III. It defines the shape of the subshell i.e. electron cloud.
The angular momentum quantum number, l, also governs the number of angular nodes that pass through the nucleus. When the angular part of the wave function goes through 0 and changes sign, an angular node (planar or conical) is detected.
| Sub-shell | Shape | Spectroscopic term | |
| s | Spherical |  | Sharpe |
| p | Dumb-bell |  | Principle |
| d | Double dumbbell | 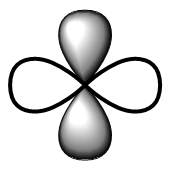 | Diffuse |
| f | Complex | Fundamental |
IV. It determines the number of orbitals present in a subshell.
The number of orbital presents is given by 2l + 1
| Sub shell | Number of orbitals (2l + 1) |
| s | 2 x 0 + 1 = 1 |
| p | 2 x 1 + 1 = 3 |
| d | 2 x 2 + 1 = 5 |
| F |
V. The energy of different subshells in multi-electron atoms
The energy levels in hydrogen and hydrogen-like atoms (one electron system) are determined only by the principle quantum number. However, these energy levels are also divided according to the magnitude of l. So, higher-order quantum states are positioned above lower-order quantum states. For instance, the energy of the 2s orbital is lower than that of the 2p orbital, while the 3d orbital exists in a higher position than the 3p orbital.
Magnetic quantum number
The magnetic quantum number was developed to explain the Zeeman effect, which includes the splitting of spectral lines in the presence of a magnetic field. The further splitting of these spectral lines shows that the energy levels (sub-shells) are subdivided further. The sub-shell (electron cloud) is further separated into several locations where the possibility of detecting an electron is high. These are known as atomic orbitals. To represent the orbital, a third quantum number termed magnetic quantum number, designated by ml or m, was established.
In other words, the quantum number m is nothing more than the permitted effects of orbital angular momentum in the z-direction. The term “magnetic quantum number” refers to how m affects the energy of an electron in a magnetic field. All spherical harmonics corresponding to different arbitrary values of m will be identical in the absence of such a field.
The magnetic quantum number is determined by the value of l. It can take any integral value between + l and – l, including zero. i.e., m = + l …0…- l
For example, if n = 4 and l = 3 in an atom, the magnetic quantum number can be -3, -2, -1, 0, +1, +2, and +3.
| Value of azimuthal quantum number (l) | Sub – shell | Number of orbitals (2l + 1) | The possible value of ml |
| 0 | s | 2 x 0 + 1 = 1 | 0 |
| 1 | p | 2 x 1 + 1 = 3 | -1, 0, and 1 |
| 2 | d | 2 x 2 + 1 = 5 | -2, -1, 0, 1, and 2 |
| 3 | F | 2 x 3 + 1 = 7 | -3, -2, -1, 0, 1, 2, and 3 |
Significance of Magnetic Quantum Number (m)
The spatial orientation of electron clouds, i.e., their orbital around the nucleus in three dimensions, is determined by magnetic quantum numbers. In other words, it indicates the number of orbitals associated with that subshell.
Examples:
For s sub-shell
I=0, m = 0
There is only one value of m for the s sub-shell. As a result, a subshell has just one type of spatial orientation. That is, it only has one orbital. In other words, it is not subdivided into orbitals.
The s-orbital has a spherically symmetrical shape. It denotes that the possibility of finding an electron is the same along all three axes surrounding the nucleus.
For p sub-shell
l = 1
m = +1, 0 and -1
Three values for the p sub-shell indicate that it has three types of spatial orientation, i.e., three orbitals. All p-orbital have the same shape, which is a dumbbell, but their directions vary. Since they are positioned along the X, Y, and Z axes lying perpendicular to one another, they are given the designations px, py, and pz.
Spin quantum number
The spin quantum number was proposed to explain the observed fine structure (doublet) in the alkali metal spectrum. According to Uhlenbeck and Goudsmit (1925), this is due to electron spin rotation about its axis.
The spin quantum number cannot be calculated simply by solving the Schrodinger wave equation. Paul Dirac invented relativistic quantum mechanics in 1929, and the solution produced a result equivalent to electronic spin. While spinning around the nucleus, the electron spins about its axis. The electron can spin in either a clockwise or anticlockwise way. Ulhlenbeck and Goudsmit introduced a fourth quantum number termed spin quantum number, represented by s or ms, to express the direction of spin.
The electron spin quantum number is independent of n, l, and ml values. This number’s value indicates the direction in which the electron is spinning. The electron spin quantum number can have values between +1/2 and -1/2.
A positive number of ms indicates an upward spin on the electron, which is also known as spin up’ and is indicated by the symbol ↿.
A negative number of ms indicates a downward spin on the electron, which is also known as spin down’ and is indicated by the symbol ⇃.
Some questions
I. Write all possible quantum numbers for the valence electrons of sulfur.
Valence shell electronic configuration of sulfur (S) = 3s2, 3p4
for 3s, n = 3, l = 0, m = 0
for 3p, n = 3, l = 1, m = +1, 0, -1
| Electron on valence shell | n | l | ml | ms |
| 1st | 3 | 0 | 0 | +1/2 |
| 2nd | 3 | 0 | 0 | -1/2 |
| 3rd | 3 | 1 | +1 | +1/2 |
| 4th | 3 | 1 | 0 | +1/2 |
| 4th | 3 | 1 | -1 | +1/2 |
| 6th | 3 | 1 | +1 | -1/2 |
II. Explain why 1p, 2d, and 3f orbital do not exist.
For 1p
n = 1, l = 0
This corresponds to n=1. In other words, the initial shell only contains a s orbital. As a result, p orbitals are not permitted to accommodate.
For 2d
n = 2, l = 0, 1 (s and p orbital)
For n = 2, l has 0 and 1 values. It denotes that this shell can only contain s and p orbitals. As a result, d orbitals are not permitted in the second shell (L-Shell).
For 3f
n = 3, l = 0, 1 and 2 (s, p and d orbital)
For n = 3, l has 0,1 and 2 values. It denotes that this shell can only contain s, p, and d orbitals. As a result, f orbitals are not permitted in the third shell.
References
- Lee J. D. (1977). A new concise inorganic chemistry (3d ed.). Van Nostrand Reinhold. Retrieved May 31 2023 from https://archive.org/details/newconciseinorga00leej.
- https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Quantum_Mechanics/10%3A_Multi-electron_Atoms/Quantum_Numbers_for_Atoms.
- https://byjus.com/chemistry/quantum-numbers/#:~:text=The%20set%20of%20numbers%20used,are%20given%20by%20quantum%20numbers.
- https://www.angelo.edu/faculty/kboudrea/general/quantum_numbers/Quantum_Numbers.pdf.
- https://www.geeksforgeeks.org/quantum-numbers/.
- http://www.adichemistry.com/general/atomicstructure/qnum/quantum-numbers.html.
