The Schrodinger wave equation describes a particle’s behavior in a force field or changing a physical parameter over time. Erwin Schrodinger was awarded the Nobel Prize in 1933 for his discovery.
Erwin Schrodinger developed a wave equation using de-Broglie’s theory of particle-wave duality. Schrodinger wave equation describes the behavior of tiny particles such as electrons in terms of waves. The discovery of the Schrodinger wave equation gave a theory from which atomic phenomena such as energy levels of atoms, chemical bonding, and so on could be estimated more correctly and quantitatively.
The Schrodinger wave equation is a mathematical expression that describes the energy and position of an electron in space and time while accounting for the electron’s matter wave nature inside an atom.
The Schrodinger wave equation describes the wave characteristics of an electron in terms of its position, mass, total energy, and potential energy. The equation is based on a wave function that describes the motion of an electron wave through space.
The Schrodinger wave equation can be written in many forms, one of which is written as,
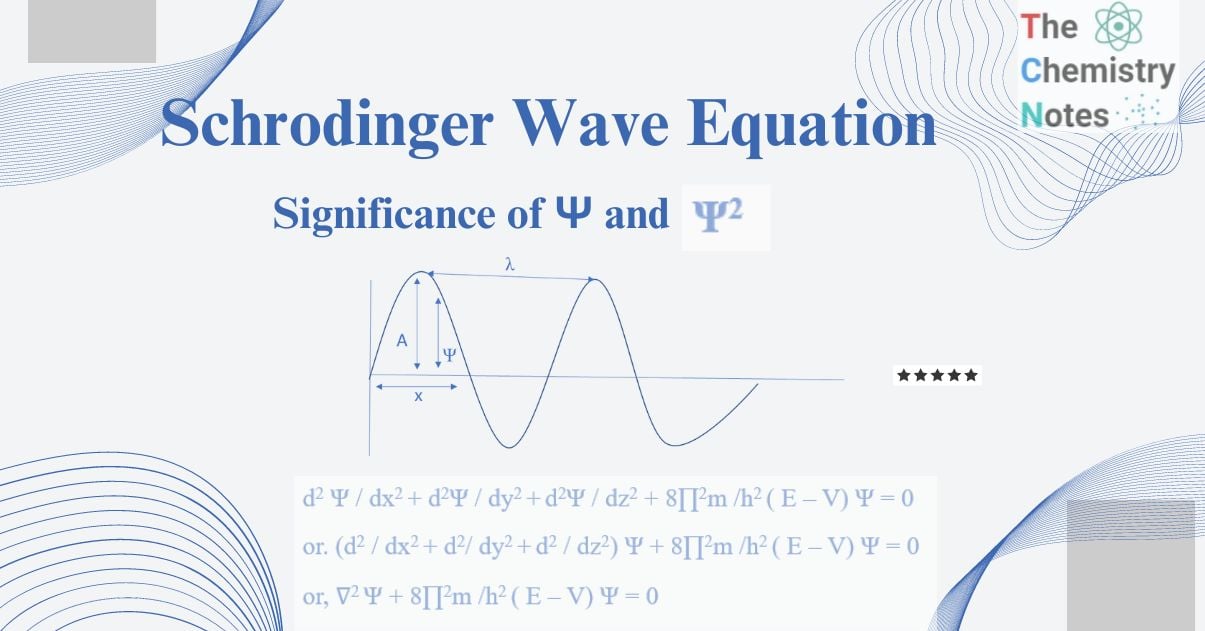
d2 Ψ / dx2 + d2Ψ / dy2 +d2Ψ / dz2 + 8∏2m /h2 ( E – V) Ψ = 0
or. (d2 / dx2 + d2/ dy2 +d2 / dz2) Ψ + 8∏2m /h2 ( E – V) Ψ = 0
or, ∇2 Ψ + 8∏2m /h2 ( E – V) Ψ = 0
Where, x, y, z = Space coordinates of the electron wave with respect to the nucleus.
∇2 = Laplacian operator
m = mass of the electron
h = Planck’s constant
E = Total energy of an electron
V = potential energy of an electron
E -V = kinetic energy of the electron
Ψ = a mathematical function called a wave function. It represents the amplitude of the electron wave surrounding the nucleus at different places in three dimensions. The magnitude that characterizes the de Broglie wave is referred to as the wave function.
Interesting Science Videos
Derivation of Schrodinger wave equation
A simple harmonic wave motion (such as for a vibrating string) can be described by the equation.
Ψ = A sin 2∏x / λ……………(I)
Ψ = Amplitude of a vibrating wave whose magnitude is varying, with respect to distance x from the origin and called a wave function.
A = a constant representing the maximum amplitude of Ψ.
X = displacement of the wave along the x-axis.
Λ = wavelength of the vibrating wave.
Differentiating equation (I) with respect to x, we get
or, d Ψ/dx = ( 2∏ / λ) A cos 2∏x / λ
Differentiating again, we get,
or, d2 Ψ/dx2 = (2∏ / λ) ( 2∏ / λ) A (-sin 2∏x / λ)
or, d2 Ψ/dx2 = – 4∏2 / λ2 A sin 2∏x / λ
or, d2 Ψ /dx2 = – 4∏2 / λ2 Ψ ( Ψ = A sin 2∏x / λ)
or, d2 Ψ /dx2 + 4∏2 / λ 2 Ψ = 0…………(II)
There are classical wave equations that describe the wave motion of any particle vibrating along the x-axis. Since electron behaves as a standing wave around the nucleus, the classical wave equation
is also applied to electron waves.
We know,
Total energy (E) = Kinetic energy + Potential energy
= ½ mv2 + V…………(III)
here, m = Mass of electron
v = Velocity of electron
V = Potential energy of an electron
From de- Broglie equation
Λ = h/mv
or, mv = h / λ
or, m2v2 = h2 / λ2
or, mv2 = h2 / λ2m
or, ½ mv2 = h2 / 2λ2m
Substituting the value of ½ mv2 in equation (III)
E = h2 / 2λ2m + V
or, h2 / 2 λ2m = (E- V)
1/ λ2 = 2m / h2 (E -V)
Substituting the value of 1/ λ2 in equation (II) we get,
d2 Ψ /dx2 + 8∏2m / h 2 ( E-V) Ψ = 0
This is one dimensional Schrodinger wave equation, If the electron wave is moving along three axes x, y, and z, then the wave motion of an electron is described by the equation:
d2 Ψ /dx2 + d2 Ψ /dy2 + d2 Ψ /dz2 + 8∏2m / h 2 ( E-V) Ψ = 0
This is the Schrodinger wave equation and it is a second-order differential equation.
Significance of Ψ and Ψ2
Ψ is a mathematical function known as a wave function. It displays the amplitude of an electron wave as it travels around the nucleus in three dimensions.
The Heisenberg uncertainty principle states that the electron’s location is unknown. Such uncertain properties can be studied using a probability function. Ψ does not represent the probability of detecting an electron near the nucleus. This is due to the fact that it can have both positive and negative values, whereas the probability can be either positive or zero, but never negative. As a result, Ψ has no physical meaning.
However, the square of i.e. Ψ i.e. Ψ 2 always has positive values, therefore the internal structure of an atom (i.e. charge distribution) from a wave mechanical perspective can be represented by Ψ2.
Ψ 2 denotes the likelihood of detecting an electron in an exceedingly small volume surrounding the nucleus in three dimensions. The value of Ψ 2 alters depending on the space location. As a result, the probability of finding the electron in different places varies. This is consistent with the certainty principle, which gave a death blow to Bohr’s concept of sharply defined orbits.
It is obvious that Ψ 2 varies from place to place; there must be a space or region where its value is maximum. In the region at which Ψ 2 is maximum, the probability of finding an electron over
that region is also maximum. “The space or region around the nucleus where the probability of finding an electron is greatest is known as the atomic orbital.”. Hence Ψ 2 represents the atomic orbital.
Summary
I. Ψ is a wave function that refers to the amplitude of an electron wave, i.e. the probability amplitude. It has no physical significance. The wave function could be positive, negative, or imaginary.
II. Ψ 2 is known as probability density determines the possibility of finding an electron at a certain place within the atom. This means that if:
- Ψ 2 is zero, the chances of finding an electron at that position are negligible.
- Ψ 2 is high, the probability of discovering an electron is high, indicating that the electron has been there at that location for a long period.
- Ψ 2 is low, probability of finding an electron is minimal, indicating that the electron is only present for a short period of time.
Conditions for the acceptable Wave Function Ψ
(Characteristics of Eigen wave functions)
As a second-order differential equation, the solution of the Schrodinger wave equation for an electron may produce a number of values for Ψ. Many of these values of Ψ are imaginary and have no physical meaning. However, only values that are physically significant and adhere to specific system requirements will be accepted. Such acceptable wave function values are known as Eigen functions (German, Eigen = appropriate, acceptable).
The discrete energy value (E) given by a particular Eigen function (the wave function which is
acceptable) is called Eigen value. Hence every wave function is not an Eigen function.
In order to get an acceptable wave function i.e., Eigen function, it should follow the following conditions.
- The wave function, Ψ, must be continuous. A real wave function is continuous.
- The wave function, Ψ, must be finite, and having an infinite value at any place means that the electron is locked there. This contradicts our wave representation.
- The wave function, Ψ, must be single valued ie., at a given point there can’t be more than one value of Ψ.
- The time wave function, Ψ, must be normalized ie., the probability of finding an electron over all the space from – ∞ to +∞ must be equal to one.
+∞
∫ Ψ 2 dx, dy, dz =1
– ∞
5. d2 Ψ / dx2, d2Ψ / dy2 , and d2Ψ / dz2 must be continuous function of x. y, and z respectively.
References
- Lee J. D. (1977). A new concise inorganic chemistry (3d ed.). Van Nostrand Reinhold. Retrieved June 2 2023 from https://archive.org/details/newconciseinorga00leej.
- S.D. Gautam, M. K. Prasad. D. P. Bhattarai and B. R. Pandey (2074). Fundamental chemistry, Heritage publishers, and distributors.
- https://byjus.com/jee/schrodinger-wave-equation/.
- https://www.vedantu.com/physics/schrodinger-wave-equation.
- https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Book%3A_Quantum_States_of_Atoms_and_Molecules_(Zielinksi_et_al)/03%3A_The_Schr%C3%B6dinger_Equation.
- https://www.astro.uvic.ca/~jwillis/teaching/phys215/phys215_lecture4.pdf.
